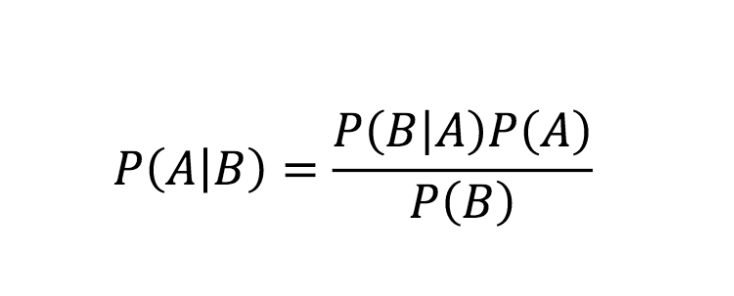What Is Binomial Probability Distribution

Binomial bernoulli normal probability binomiale distribuzione variance pmf binomialverteilung variables discreta plot parameter

Table of Contents

Have you ever wondered what the Binomial Probability Distribution is and how it can help you solve probability problems? Understanding this concept can be challenging, but it is essential for anyone working with probability and statistics. In this article, we will cover the basics of the Binomial Probability Distribution and how it can be used to solve problems in real-world situations.

When it comes to probability, one of the most significant barriers that people face is how to calculate the probability of an event happening a certain number of times. For example, suppose you want to know the probability of winning two out of three games of chance. This is where the Binomial Probability Distribution comes in handy, as it provides a way to calculate the probability of a specific number of successes in a given number of trials.

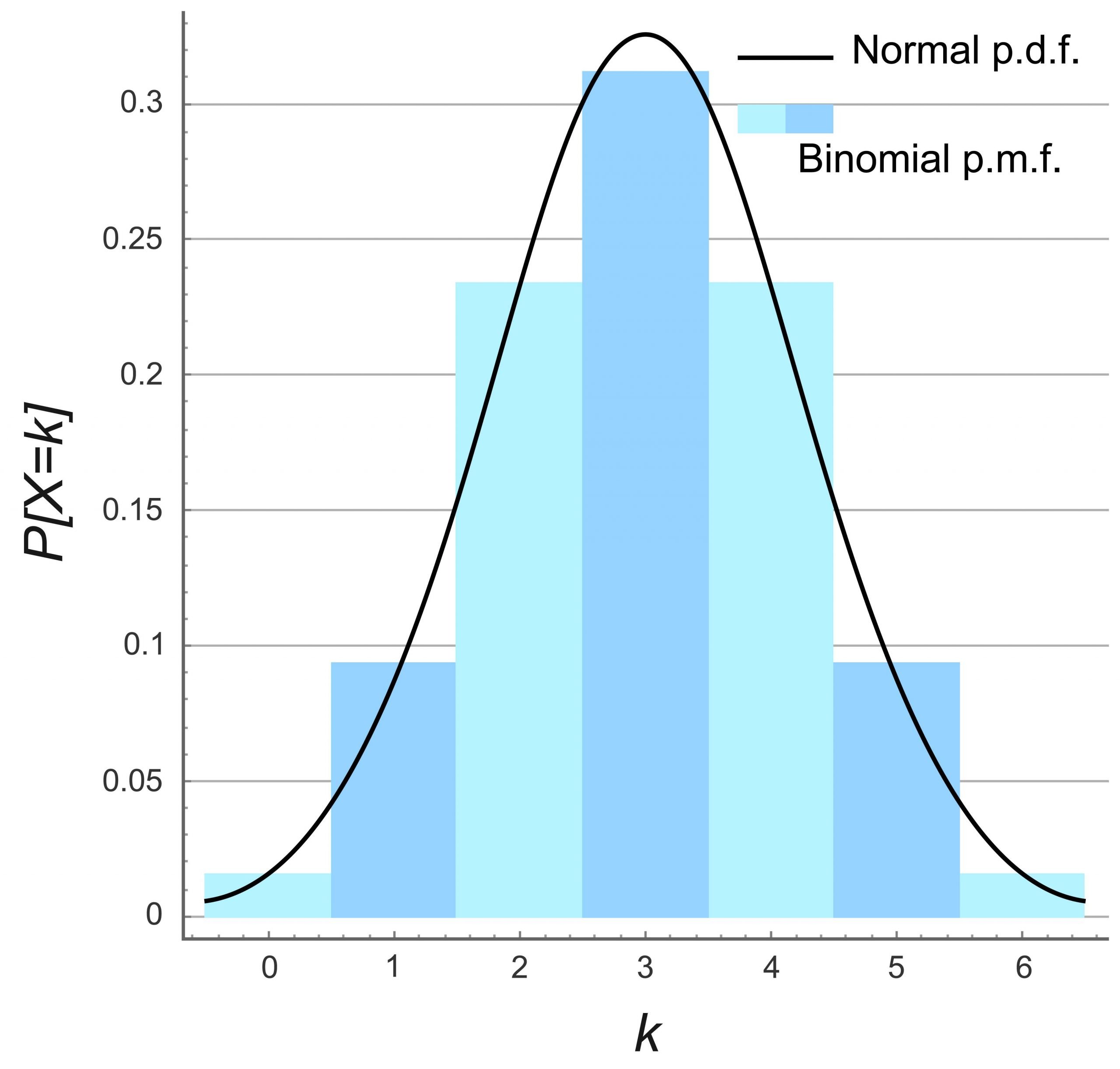
The Binomial Probability Distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials, each with the same probability of success. It is a common tool used in various fields, such as finance, engineering, and science, to model experiments with two possible outcomes, such as success or failure.

In summary, the Binomial Probability Distribution is a statistical tool used to calculate the probability of a specific number of successes in a given number of trials.

What Is Binomial Probability Distribution and Its Applications?

The Binomial Probability Distribution has many real-world applications. For example, it can be used to calculate the probability of flipping heads or tails in a coin toss, the probability of passing or failing a test, or the probability of winning or losing a game of chance. It can also be used in finance to model the probability of a stock increasing or decreasing in value over a specific period.

As a data scientist, I’ve used the Binomial Probability Distribution in many projects, such as predicting the likelihood of a customer churn event or the probability of a patient developing a specific health condition.

One example of using the Binomial Probability Distribution came up when I was working with a marketing team. We needed to calculate the probability of a customer purchasing a specific product after receiving a promotional email. By using the Binomial Probability Distribution, we were able to estimate the probability of a product purchase based on the number of customers who opened the promotional email.

How to Calculate Binomial Probability Distribution?

The Binomial Probability Distribution uses a specific formula to calculate the probability of a specific number of successes in a fixed number of trials. The formula is:

Where:

• p = probability of success on each trial
• n = total number of trials
• x = number of successes

For example, suppose you are playing a game where you need to roll a six on a six-sided die. The probability of rolling a six is 1/6. If you roll the die six times, what is the probability that you will roll two sixes?

To solve this problem using the Binomial Probability Distribution formula:

• p = 1/6
• n = 6
• x = 2

Plugging these values into the formula, we get:

Therefore, the probability of rolling two sixes in six rolls is approximately 16%.

Binomial Probability Distribution Properties

There are some essential properties of the Binomial Probability Distribution that are important to understand:

• The trials in the experiment must be independent.
• There can only be two outcomes of each trial.
• The probability of success on each trial must be the same for all the trials.
• The number of trials in the experiment must be fixed.

Binomial Probability Distribution vs. Poisson Distribution

One common question that arises is how the Binomial Probability Distribution differs from the Poisson Distribution. The main difference is that the Binomial Distribution is used to model a discrete number of events with a fixed number of trials, while the Poisson Distribution is used to model the occurrence of rare events over a continuous interval. The Poisson Distribution is based on the mean number of events per interval, while the Binomial Distribution is based on the probability of each event occurring.

Conclusion of What Is Binomial Probability Distribution

The Binomial Probability Distribution is a statistical tool that helps us calculate the probability of a fixed number of successes in a given number of trials. It is commonly used in various fields, including finance, science, and engineering, to model experiments with two possible outcomes. Understanding this concept is essential for anyone working with probability and statistics as it has many real-world applications.

Question and Answer:

1. What is the Binomial Probability Distribution?

The Binomial Probability Distribution is a statistical tool used to calculate the probability of a specific number of successes in a given number of trials.

2. What are the applications of the Binomial Probability Distribution?

The Binomial Probability Distribution has many real-world applications, such as calculating the probability of flipping heads or tails in a coin toss, passing or failing a test, or winning or losing a game of chance. It can also be used in finance to model the probability of a stock increasing or decreasing in value over a specific period.

3. What is the formula for the Binomial Probability Distribution?

The formula for the Binomial Probability Distribution is: P(X=x) = (n C x) * p^x * (1-p)^(n-x).

4. How does the Binomial Probability Distribution differ from the Poisson Distribution?

The main difference is that the Binomial Distribution is used to model a discrete number of events with a fixed number of trials, while the Poisson Distribution is used to model the occurrence of rare events over a continuous interval. The Poisson Distribution is based on the mean number of events per interval, while the Binomial Distribution is based on the probability of each event occurring.

Gallery

PPT - Binomial Probability Distribution 1. The Experiment Must Have A

_{^{Photo Credit by: bing.com / binomial probability distribution formula experiment trials fixed number method must ppt powerpoint presentation qn px slideserve}}

PPT - Binomial Probability Distribution PowerPoint Presentation, Free

_{^{Photo Credit by: bing.com / binomial distribution probability mean variance ppt success standard deviation cdf trials powerpoint presentation}}

Bernoulli Random Variables And The Binomial Distribution In Probability

_{^{Photo Credit by: bing.com / binomial bernoulli normal probability binomiale distribuzione variance pmf binomialverteilung variables discreta plot parameter}}

Binomial Probability Distribution Tutorial

_{^{Photo Credit by: bing.com / binomial probability formulas calculate successes onlinemathlearning trials tosses fraction bernoulli roll}}

Binomial Probability Distribution - Data Science Kernel

_{^{Photo Credit by: bing.com / distribution binomial probability statistics}}