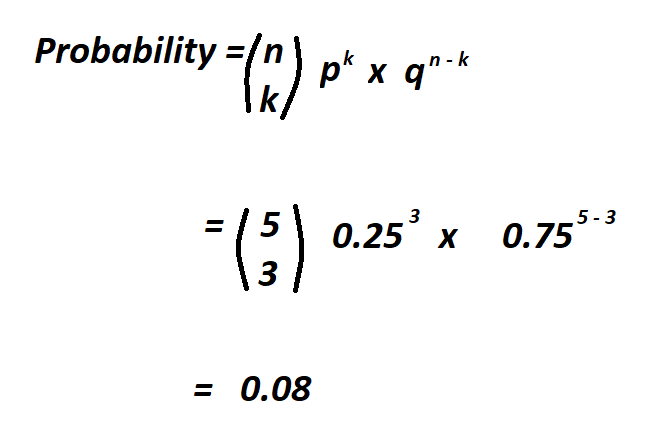Distribution binomial probability statistics

Table of Contents

If you’ve ever wondered about the likelihood of an event happening multiple times under specific conditions, you may have stumbled upon the concept of a binomial probability distribution. This statistical tool is commonly used in fields such as finance, engineering, and biology to calculate the probability of specific outcomes.

Whether you’re a math enthusiast or not, understanding the basics of the binomial probability distribution can be a helpful skill in analyzing data and making informed decisions.

What Is A Binomial Probability Distribution?

A binomial probability distribution is a statistical tool used to calculate the probability of a specific number of occurrences of an event within a fixed number of trials, assuming that the probability of success remains the same for each trial. In other words, it is used when there are only two possible outcomes for each event, such as success or failure, or heads or tails.

For example, suppose you want to know the probability of flipping a coin five times and getting heads three times. A binomial probability distribution can help you calculate the likelihood of this happening.

Personal Experience with Binomial Probability Distribution

As an e-commerce business owner, I frequently use the binomial probability distribution to calculate the likelihood of success for a particular marketing campaign. By analyzing data from previous campaigns, I can estimate the probability of a specific number of conversions based on a fixed number of ad impressions, which helps me make informed decisions about budget allocation and campaign strategies.

Applications of Binomial Probability Distribution

The binomial probability distribution has a wide range of applications across various industries. In finance, it is used to calculate the probability of events such as stock price increases or decreases. In engineering, it is used to calculate the probability of equipment failures in a fixed number of trials. In biology, it is used to calculate the probability of gene mutations in a specific population.

How to Calculate Binomial Probability Distribution?

The formula for calculating binomial probability distribution is:

Where:

• P(x) is the probability of x successes in n trials
• n is the number of trials
• x is the number of successes
• p is the probability of success for each trial
• q is the probability of failure for each trial, which is equal to 1-p

Example Calculation

Suppose you flip a coin 10 times and want to know the probability of getting heads exactly 7 times. If the probability of heads is 0.5 for each flip, the calculation would be:

P(7) = (10 choose 7) * 0.5^7 * 0.5^3 = 0.117

Therefore, there is a 11.7% chance of getting heads exactly 7 times out of 10 flips.

Question and Answer

Q: What are the assumptions of binomial probability distribution?

A: The assumptions are that there are a fixed number of trials, each trial has only two possible outcomes, the probability of success remains constant for each trial, and the trials are independent.

Q: What is the difference between binomial distribution and normal distribution?

A: Binomial distribution is used when there are only two possible outcomes for each event, while normal distribution is used when there are numerous possible outcomes. Additionally, normal distribution assumes that the data is continuous, while binomial distribution assumes that the data is discrete.

Q: Can binomial probability distribution be used for small sample sizes?

A: Yes, binomial probability distribution can be used for small sample sizes as long as the assumptions are met. However, as n gets smaller, the approximation of the binomial distribution to the normal distribution becomes less accurate.

Q: What is the importance of binomial probability distribution in hypothesis testing?

A: Binomial probability distribution is used in hypothesis testing to determine if the observed outcomes are statistically significant or if they could have occurred by chance. By calculating the probability of the outcome under the null hypothesis, we can determine the level of statistical significance and make informed decisions.

Conclusion of What Is A Binomial Probability Distribution

A binomial probability distribution is a powerful statistical tool that can be used to calculate the probability of a specific number of occurrences of an event within a fixed number of trials. By understanding the basics of binomial probability distribution and its applications, you can make informed decisions based on data analysis.

Gallery

PPT - Binomial Probability Distribution PowerPoint Presentation, Free

_{^{Photo Credit by: bing.com / binomial distribution probability mean variance ppt success standard deviation cdf trials powerpoint presentation}}

Binomial Probability Distribution Tutorial

_{^{Photo Credit by: bing.com / binomial probability formulas calculate successes onlinemathlearning trials tosses fraction bernoulli roll}}

Bernoulli Random Variables And The Binomial Distribution In Probability

_{^{Photo Credit by: bing.com / binomial bernoulli normal probability binomiale distribuzione variance pmf binomialverteilung variables discreta plot parameter}}

Binomial Probability Distribution - Data Science Kernel

_{^{Photo Credit by: bing.com / distribution binomial probability statistics}}

PPT - Binomial Probability Distribution 1. The Experiment Must Have A

_{^{Photo Credit by: bing.com / binomial probability distribution formula experiment trials fixed number method must ppt powerpoint presentation qn px slideserve}}