Probability replacement without sampling calculate inclusion under stats written following also questions
Table of Contents
Table of Contents
Are you struggling to understand Sampling Without Replacement Probability? Do you find the topic intimidating or confusing? Understanding this concept is crucial for fields like statistics, data analysis, and other related fields.
When it comes to Sampling Without Replacement Probability, many people face a few common problems. These issues might include not understanding the concept entirely, not knowing how to calculate it correctly, and not knowing how to apply the findings to real-world data analysis.
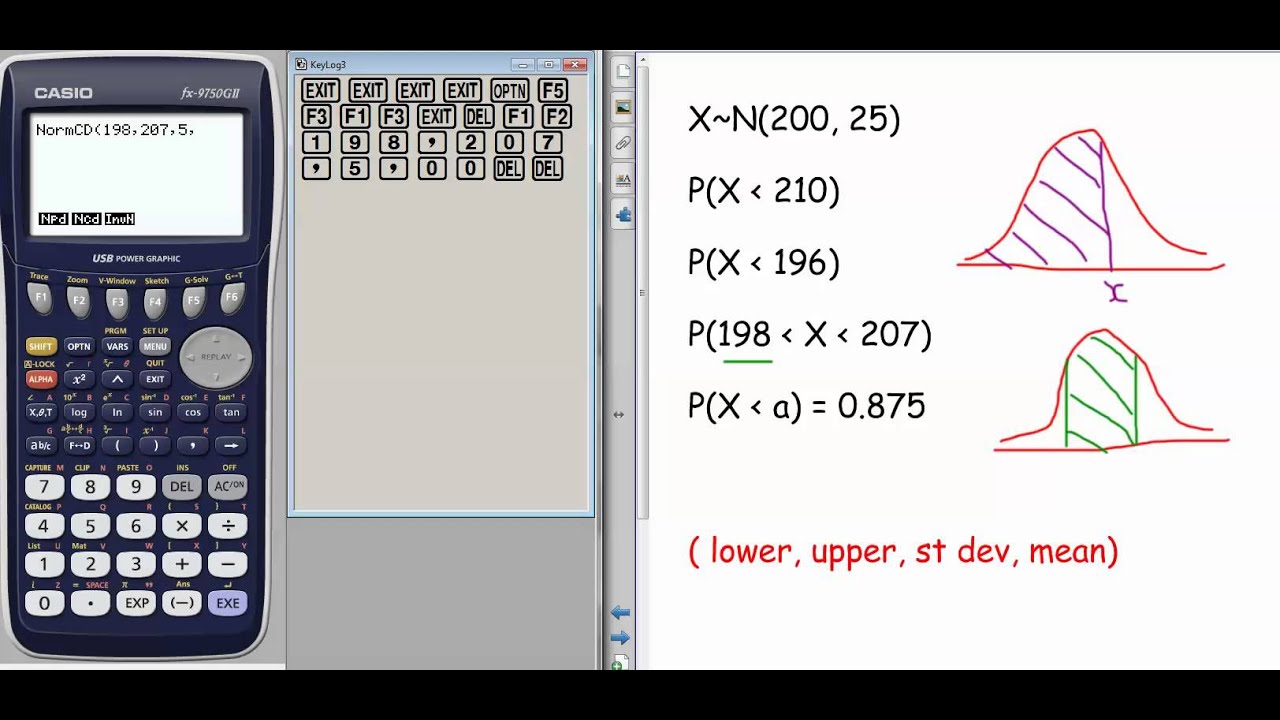
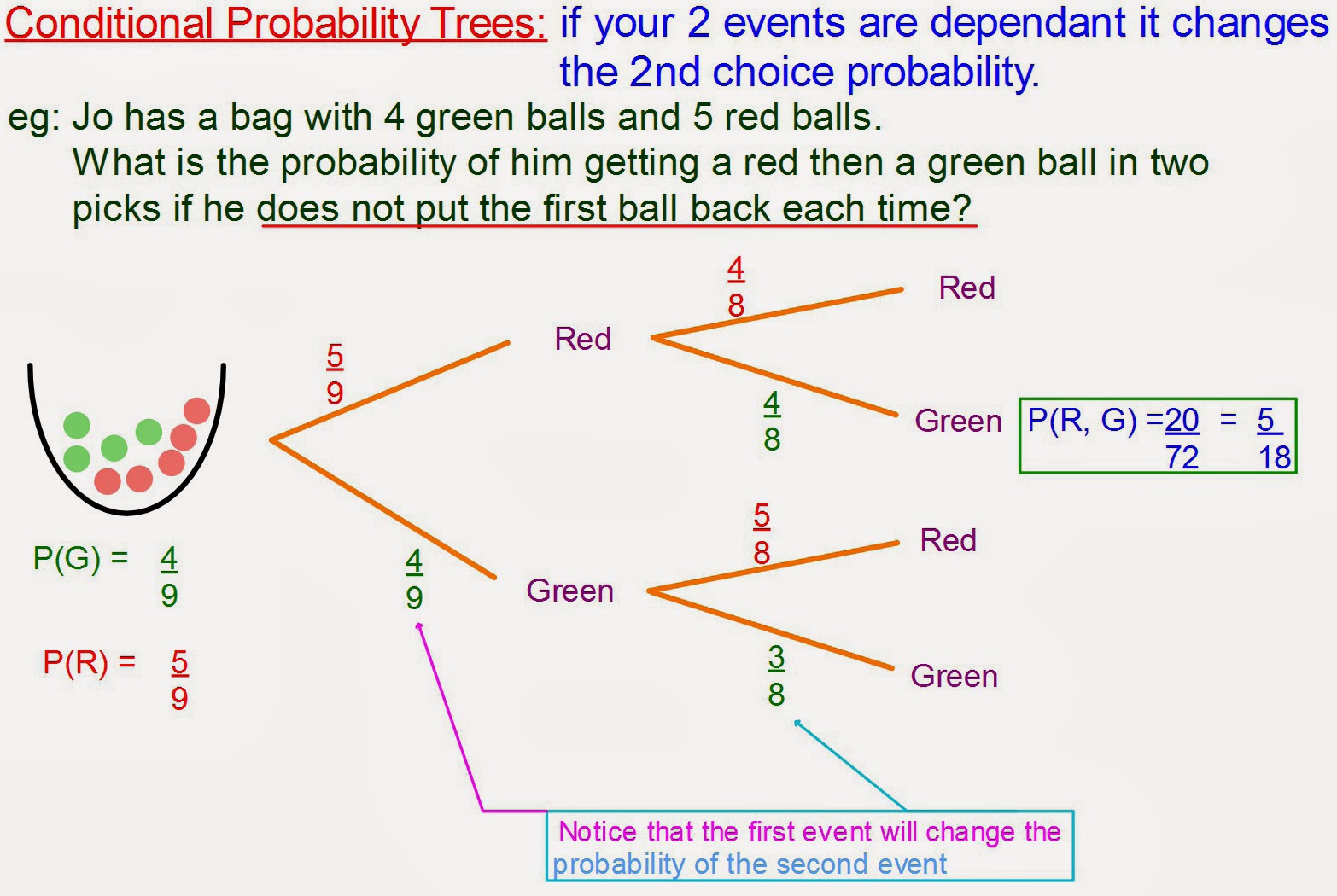
The primary goal of Sampling Without Replacement Probability is to determine the likelihood of drawing specific samples from a population without putting the sample back in the pool after each selection. Say you have a bag of marbles, and you want to determine the probability of pulling out a red marble on the first pull and a blue marble on the second. In this scenario, you’re conducting Sampling Without Replacement Probability.
In summary, Sampling Without Replacement Probability helps you determine the likelihood of selecting specific samples from a larger population without putting the sample back in the pool after every draw.
What is the Target of Sampling Without Replacement Probability?
The primary aim of Sampling Without Replacement Probability is to help you gain a better understanding of your sample data. By determining the probability of drawing samples, you can analyze the data and come up with reliable conclusions about the larger population.
Consider a group of students, where you’re trying to determine the probability of selecting specific individuals from the population. Or, imagine you’re conducting a market research study and want to determine the likelihood of drawing specific subsets from your target audience. In both scenarios, Sampling Without Replacement Probability is a crucial concept.
My Personal Experience with Sampling Without Replacement Probability
During my college education, I had to conduct a comprehensive research project on Sampling Without Replacement Probability in a real-world data analysis scenario. It was challenging to wrap my head around the concept at first, but I was eventually able to understand it better through practice problems and sample data analysis.
When applying the concept to actual data analysis, I found that Sampling Without Replacement Probability is a powerful and effective tool to determine the likelihood of selecting specific samples from larger populations. It helps you make informed conclusions about data analysis and draw accurate conclusions based on the information you have.
How does Sampling Without Replacement Probability work?
To understand Sampling Without Replacement Probability, you need to know how to calculate it. One way to calculate is by using factorials. Factorials determine the number of possible ways of selecting k elements from a population of n elements without putting the sample back. This formula is expressed as n! / (n-k)!, where n is the number of elements in the population and k is the number of elements you can select from the population.
For example, suppose you have a population of ten elements, and you’re trying to select four elements without replacement probability. The formula expresses as 10! / (10-4)! = 10! / 6! = 10 x 9 x 8 x 7 = 5,040.
Applications of Sampling Without Replacement Probability
Sampling Without Replacement Probability is used in many fields, including market research, finance, and the social sciences. In finance, traders use it to calculate the risk of individual stocks within a portfolio. Market researchers use Sampling Without Replacement Probability to determine the probability of specific subsets for the market they’re researching. Social scientists also use this concept to determine the probability of specific audiences in their research.
Why is Sampling Without Replacement Probability Essential?
Sampling Without Replacement Probability is essential to understand in several fields, mainly statistics, data analysis, and finance sectors. It enables you to calculate the probability of drawing specific samples from larger populations, leading to insightful data analysis and accurate conclusions. It is crucial for anyone dealing with data analysis to have a good understanding of Sampling Without Replacement Probability to make informed decisions based on the data presented before them.
Question and Answer
Question 1: What is Sampling Without Replacement Probability?
Sampling Without Replacement Probability is a statistical concept that determines the likelihood of selecting specific samples from a population without putting the sample back in the pool after each selection.
Question 2: What is the Formula for Sampling Without Replacement Probability?
The formula for Sampling Without Replacement Probability is expressed as n! / (n-k)!, where n is the number of elements in the population and k is the number of elements you can select from the population.
Question 3: Why is Sampling Without Replacement Probability important?
Sampling Without Replacement Probability is essential because it helps you determine the probability of selecting specific samples from larger populations, leading to insightful data analysis and accurate conclusions.
Question 4: Which fields use Sampling Without Replacement Probability?
Sampling Without Replacement Probability is used in many fields, including finance, market research, and social sciences.
Conclusion of Sampling Without Replacement Probability
In conclusion, Sampling Without Replacement Probability is a concept that anyone dealing with data analysis should understand. It determines the likelihood of drawing specific samples from larger populations without putting the sample back in the pool after each selection. By understanding this concept, you can analyze data and draw accurate conclusions about your sample. This statistical concept is used in many fields such as finance, market research, and social sciences.
Gallery
Sampling Distributions

Photo Credit by: bing.com / distributions probability
How To Calculate Inclusion Probability Under Sampling Without

Photo Credit by: bing.com / probability replacement without sampling calculate inclusion under stats written following also questions
Sampling Without Replacement Formula - Lineartdrawingssimple

Photo Credit by: bing.com /
Chapter 4 Probability Theory | Advanced Statistics I 2021 Edition
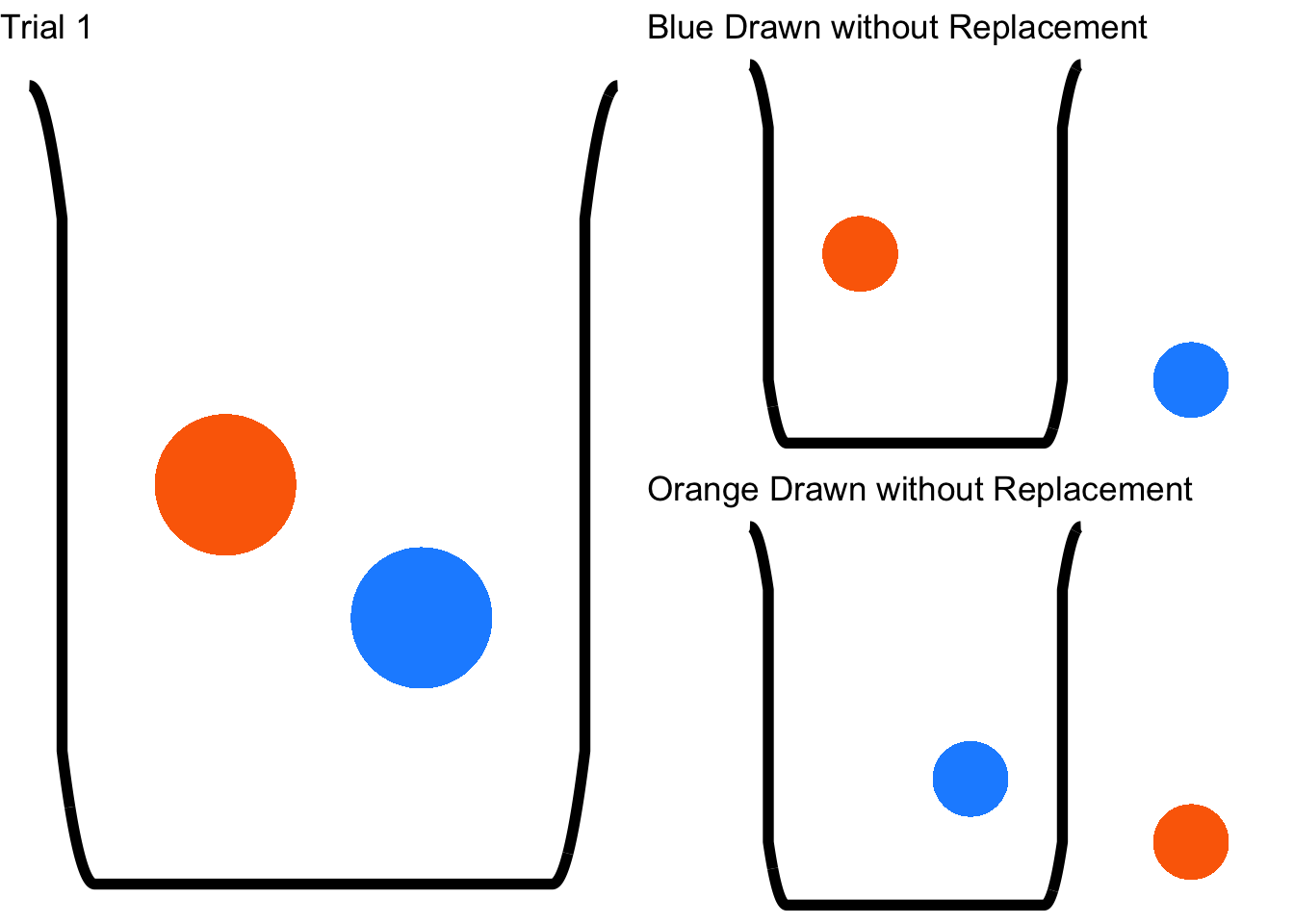
Photo Credit by: bing.com /
Sampling In SPSS - Simple Tutorial & Examples

Photo Credit by: bing.com / sampling without spss population easiest