Probability Of Multiple Independent Events

Probability theory

Table of Contents

Have you ever wondered what the probability is of multiple independent events occurring together? Imagine flipping a coin twice and rolling a dice once. What is the probability of getting heads both times and rolling a six? This is known as Probability Of Multiple Independent Events. Understanding this concept is essential in many fields, from statistics to finance.

Calculating the Probability Of Multiple Independent Events can be challenging, especially if there are several events involved. There are often pain points related to the calculation process, such as determining whether the events are truly independent or understanding how to calculate the probability of two or more independent events occurring simultaneously.

The target of Probability Of Multiple Independent Events is to determine the likelihood of two or more independent events occurring together. In other words, it is the probability that two or more events will occur at the same time.

In summary, Probability Of Multiple Independent Events involves calculating the likelihood of two or more independent events occurring simultaneously. These calculations can be challenging, and there are often pain points involved in determining the probability of multiple events. However, understanding Probability Of Multiple Independent Events is crucial in many fields.

Understanding Probability Of Multiple Independent Events

Probability Of Multiple Independent Events can be a confusing concept, but it is essential in many fields. For example, in finance, understanding the likelihood of multiple independent events occurring can help investors make better decisions. Similarly, in sports, calculating the probability of multiple independent events occurring can help coaches make more informed decisions.

One personal experience I had with Probability Of Multiple Independent Events was during a game of poker. I had two cards in my hand, and I needed a specific card to appear on the table to make a winning hand. The probability of that card appearing was low, but because the events were independent, it was still possible.

To calculate the probability of multiple independent events, you must understand the probability of each event occurring on its own. Once you have this information, you can multiply these probabilities together to get the probability of all events occurring simultaneously.

Real-World Examples of Probability Of Multiple Independent Events

One common example of Probability Of Multiple Independent Events is when flipping a coin and rolling a dice. If you flip a coin twice and roll a dice once, the probability of getting heads both times and rolling a six is:

1/2 x 1/2 x 1/6 = 1/24

Another example of Probability Of Multiple Independent Events is when drawing cards from a deck. If you draw two cards from a standard deck of cards, the probability of getting a king and then an ace is:

4/52 x 4/51 = 1.22%

Dependent vs. Independent Events

The difference between dependent and independent events is crucial in Probability Of Multiple Independent Events. In an independent event, the probability of one event occurring does not affect the probability of another event occurring. In contrast, in a dependent event, the probability of one event occurring does affect the probability of another event occurring.

For example, when drawing cards from a deck, the probability of drawing an ace changes depending on whether another ace has already been drawn. In this case, the events are dependent, and the calculation of Probability Of Multiple Independent Events becomes more complicated.

Calculating Probability Of Multiple Independent Events

To calculate Probability Of Multiple Independent Events, you must first determine whether the events are independent or dependent. If the events are independent, you can simply multiply the probability of each event occurring together. If the events are dependent, the calculation becomes more complex and may require a different formula or approach.

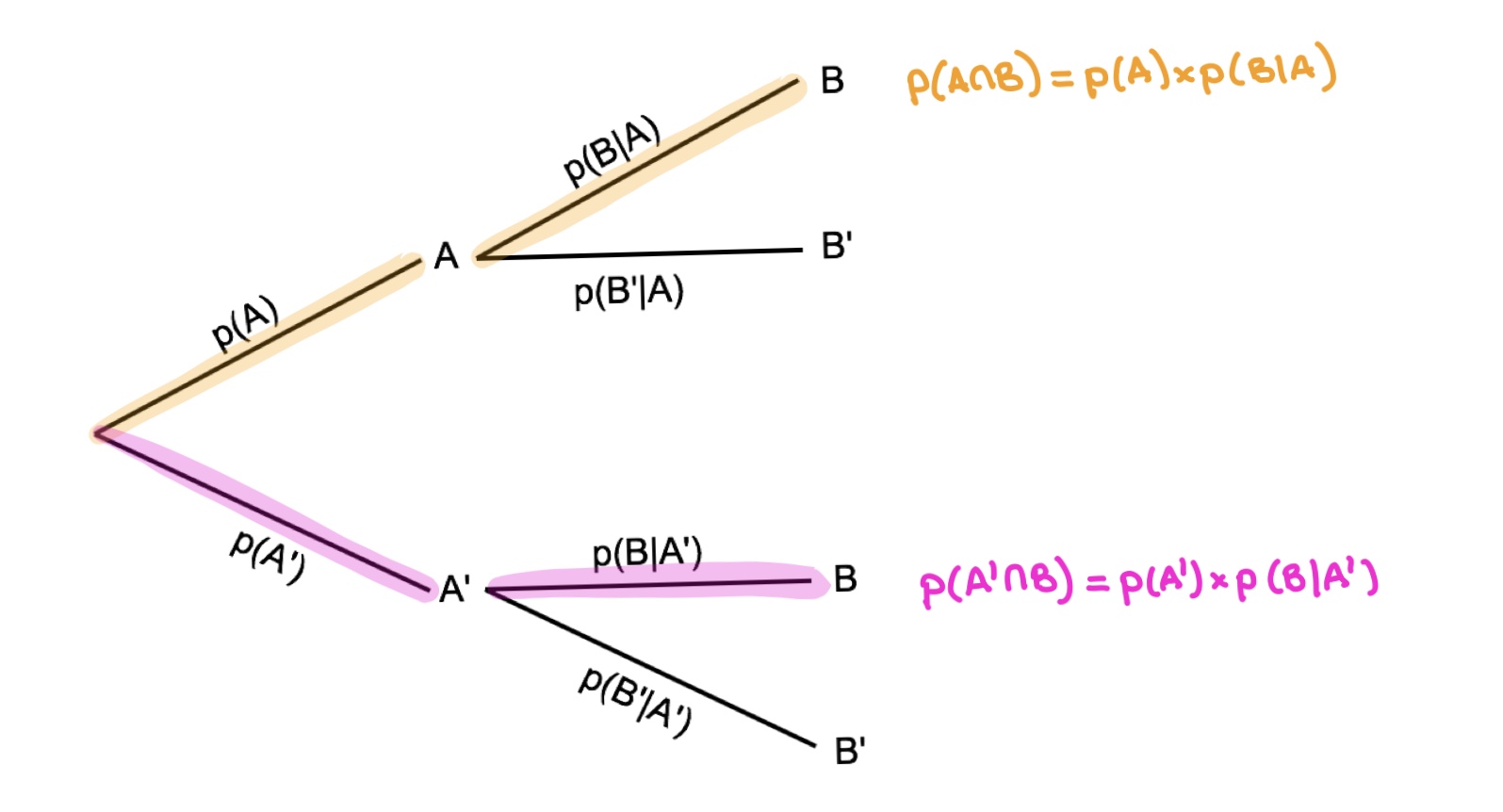
One strategy for calculating Probability Of Multiple Independent Events is to use a probability tree diagram. This diagram can help you visualize the different possible outcomes and calculate the probability of each event occurring.

FAQ About Probability Of Multiple Independent Events

Here are four common questions and answers about Probability Of Multiple Independent Events:

Q: What is the formula for calculating Probability Of Multiple Independent Events?

A: The formula for calculating Probability Of Multiple Independent Events is P(A and B) = P(A) x P(B).

Q: Can you have dependent events in Probability Of Multiple Independent Events?

A: No, Probability Of Multiple Independent Events assumes that all events are independent. If the events are dependent, the calculation of Probability Of Multiple Independent Events becomes more complicated.

Q: How do I know if events are dependent or independent?

A: Events are independent if the probability of one event occurring does not affect the probability of another event occurring. Events are dependent if the probability of one event occurring affects the probability of another event occurring.

Q: Where is Probability Of Multiple Independent Events used?

A: Probability Of Multiple Independent Events is used in many fields, from statistics and finance to sports and gaming.

Conclusion of Probability Of Multiple Independent Events

Probability Of Multiple Independent Events can be a challenging but essential concept to understand. Whether you’re an investor, athlete, or gambler, understanding the likelihood of multiple independent events occurring can help you make more informed decisions. By calculating the probability of each event occurring and multiplying them together, you can determine the likelihood of all events occurring simultaneously. As with any probability calculation, it’s important to understand whether the events are independent or dependent before proceeding with the calculation.

Gallery

The Conjunction Problem Is Not A Problem For Bayesians | Prior Probability

_{^{Photo Credit by: bing.com / dependent events probability examples independent solutions conjunction event if problem formulas following outcome}}

PPT - 12.5 Probability Of Independent & Dependent Events PowerPoint

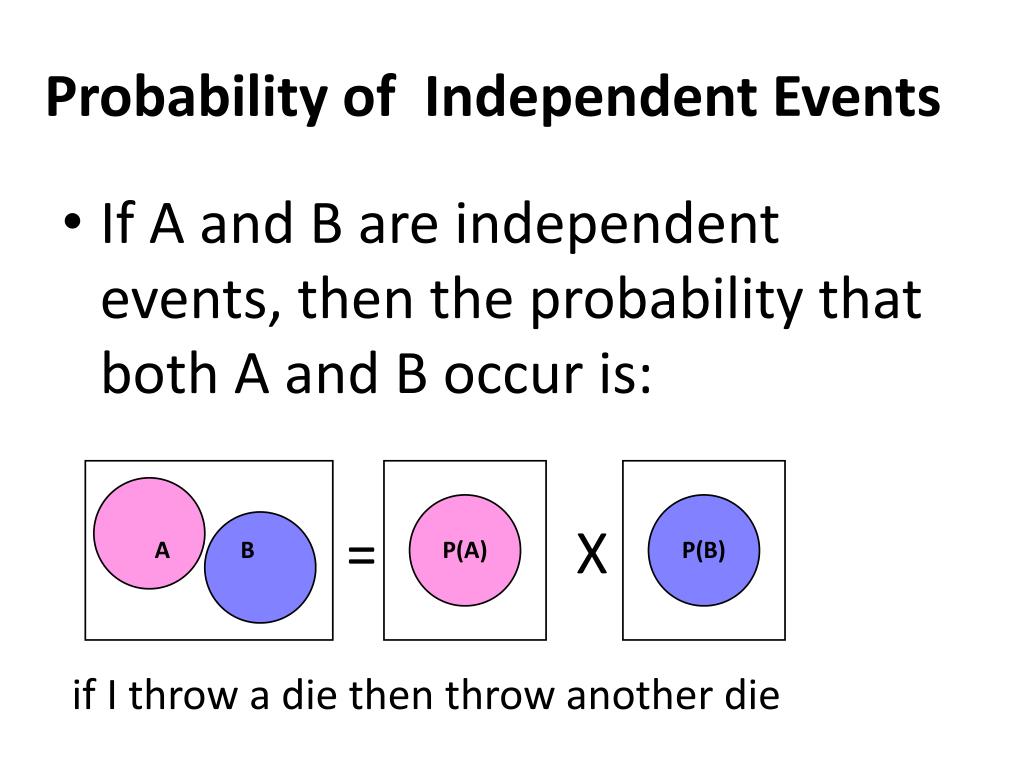
_{^{Photo Credit by: bing.com / probability independent events dependent presentation}}

Probability Theory - Independent Probabilities For Multiple Events

_{^{Photo Credit by: bing.com / independent events multiple probabilities probability definition mean math does theory questions}}

Dependent And Independent Events Probability Algebra 2 Regents - YouTube

_{^{Photo Credit by: bing.com / probability independent events dependent algebra}}

Independent And Dependent Events; Conditional Probability

_{^{Photo Credit by: bing.com / probability conditional dependent cafeteria}}