Solved compute the following binomial probabilities directly from
Table of Contents
Table of Contents
Are you struggling to understand how to compute binomial probability? This concept may seem intimidating at first, but with a little guidance, you will be able to tackle it with ease. In this article, we will explore how to compute binomial probability and related keywords that will make the process much simpler for you.
Have you ever found yourself staring at a binomial probability problem, feeling overwhelmed and unsure of where to start? Perhaps you feel like you don’t have a strong enough foundation in statistics to understand the underlying concepts. These pain points are common for anyone learning how to compute binomial probability for the first time.
At its core, binomial probability is a statistical concept used to calculate the probability of a particular outcome given a certain set of conditions. Specifically, it is used to determine the likelihood of success in a situation where there are only two possible outcomes.
So, how exactly do you compute binomial probability? Let’s go through the steps:
What is the Target of How To Compute Binomial Probability?
Before we dive into the process of computing binomial probability, it’s important to understand its target. The goal of computing binomial probability is to determine the probability of a specific number of successful outcomes in a given number of trials. For example, if you wanted to know the probability of flipping heads three times in a row, you would use binomial probability.
When I first started learning about binomial probability, I was overwhelmed by all the math involved. However, as I worked through more examples and gained a better understanding, I was able to see how it can be a powerful tool in analyzing data and making predictions.
Using the Binomial Probability Formula
To compute binomial probability, you will need to use a formula that takes into account the number of trials, the probability of success, and the number of successful outcomes you are looking for. This formula is:
Here, n represents the total number of trials, p represents the probability of success, and x represents the number of successful outcomes you are looking for.
Let’s say you were flipping a coin and wanted to know the probability of getting heads three times in a row. This would mean that n = 3 (since there are three flips), p = 0.5 (since heads and tails are equally likely), and x = 3 (since we are looking for three consecutive heads).
Plugging these values into the formula, we get:
As you can see, the probability of getting three consecutive heads is 0.125, or 12.5%.
Real-World Applications of Binomial Probability
Binomial probability has a wide range of applications in the real world. For example, it can be used in market research to forecast the success of a new product, in sports to predict the outcome of a game, and in medicine to determine the effectiveness of a treatment. Understanding how to compute binomial probability can give you valuable insights into these areas.
Practical Tips
When computing binomial probability, it’s important to keep a few practical tips in mind:
- Make sure you understand the problem and the conditions involved
- Plug the values into the formula carefully
- Check your work to make sure you didn’t make any mistakes
Tips and Tricks
To make the process of computing binomial probability even easier, here are a few tips and tricks:
- Use a calculator or computer program to do the math for you
- Practice with different examples to get a better understanding of the concept
- Try breaking the problem down into smaller parts to make it more manageable
Question and Answer
1. What is binomial probability?
Binomial probability is a statistical concept used to calculate the probability of a particular outcome given a certain set of conditions. Specifically, it is used to determine the likelihood of success in a situation where there are only two possible outcomes.
2. What is the formula for computing binomial probability?
The formula for computing binomial probability is:
P(x) = (n choose x) * p^x * (1-p)^(n-x)
Here, n represents the total number of trials, p represents the probability of success, and x represents the number of successful outcomes you are looking for.
3. What are some real-world applications of binomial probability?
Binomial probability has a wide range of applications in the real world. For example, it can be used in market research to forecast the success of a new product, in sports to predict the outcome of a game, and in medicine to determine the effectiveness of a treatment.
4. What are some practical tips for computing binomial probability?
- Make sure you understand the problem and the conditions involved
- Plug the values into the formula carefully
- Check your work to make sure you didn’t make any mistakes
Conclusion of How To Compute Binomial Probability
Computing binomial probability can seem daunting at first, but by breaking down the problem into manageable parts and using the formula, you can easily calculate the probability of a specific number of successful outcomes in a given number of trials. With the tips and tricks outlined in this article, you can gain a better understanding of this important statistical concept and its real-world applications.
Gallery
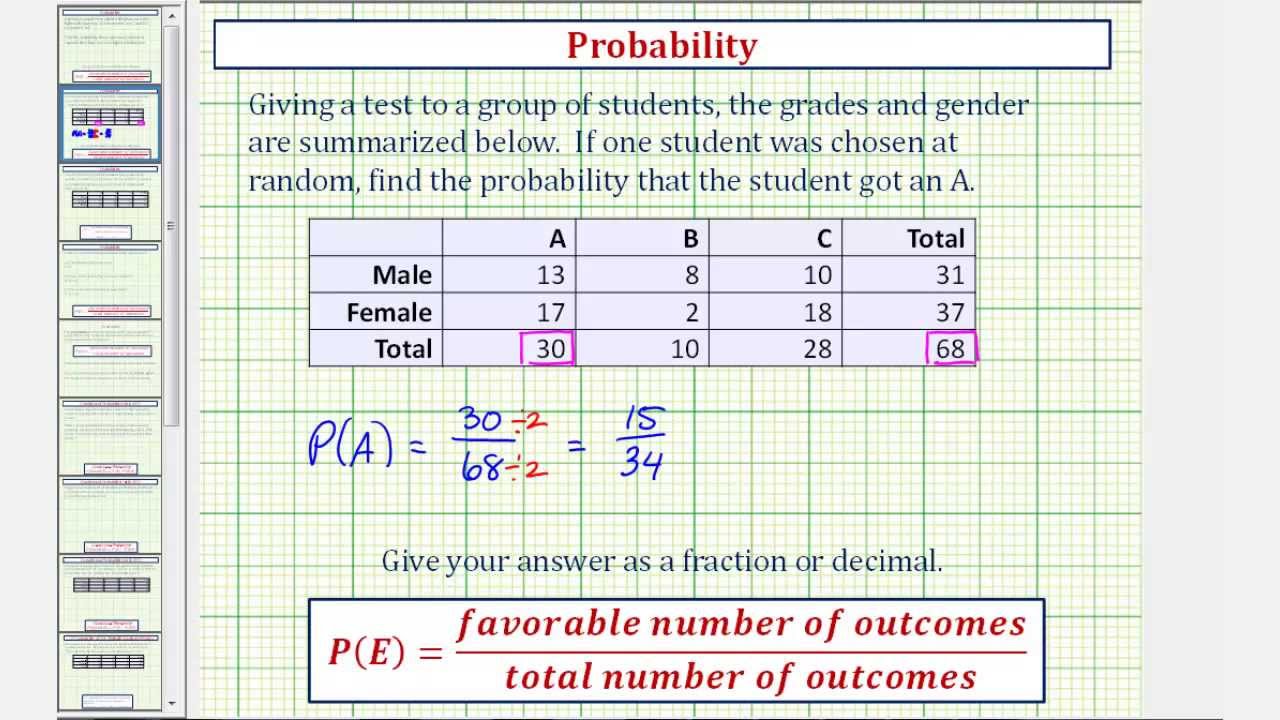
Solved: Compute The Following Binomial Probabilities Directly From
Photo Credit by: bing.com / binomial compute probabilities
Solved Compute P(X) Using The Binomial Probability Formula. | Chegg.com
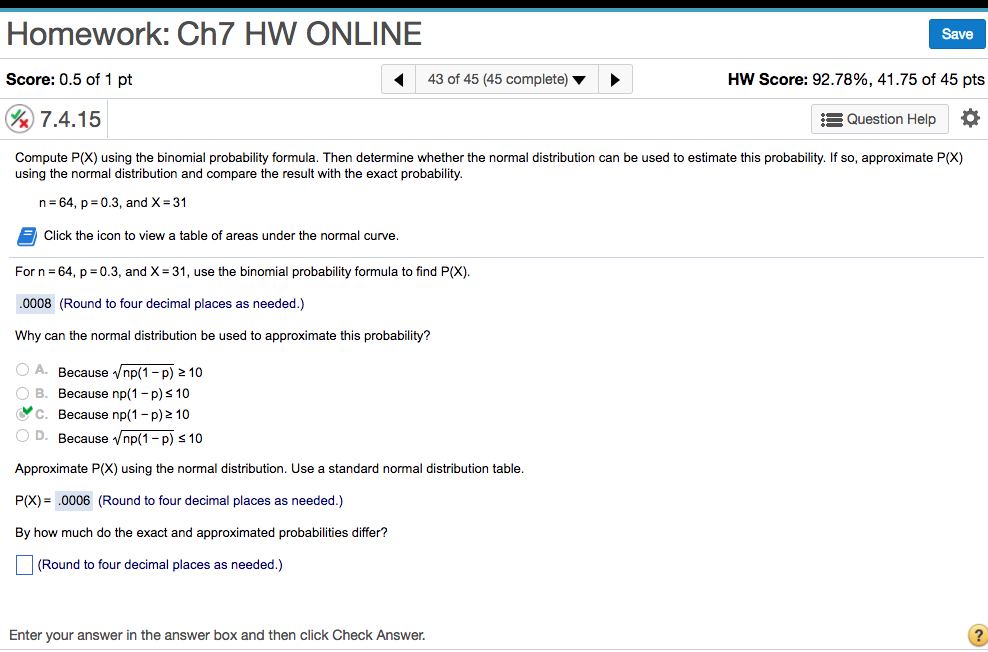
Photo Credit by: bing.com / probability using binomial compute distribution normal formula used determine whether solved answer approximate exact compare result then estimate if so
10.4 Binomial Probability Rolling A Die - YouTube
Photo Credit by: bing.com / probability binomial rolling die
Binomial Distribution Formula | Calculator (Excel Template)
Photo Credit by: bing.com / binomial probability calculator
SOLVED:Compute The Probability Of X Successes, Using The Binomial
Photo Credit by: bing.com / probability successes compute binomial
