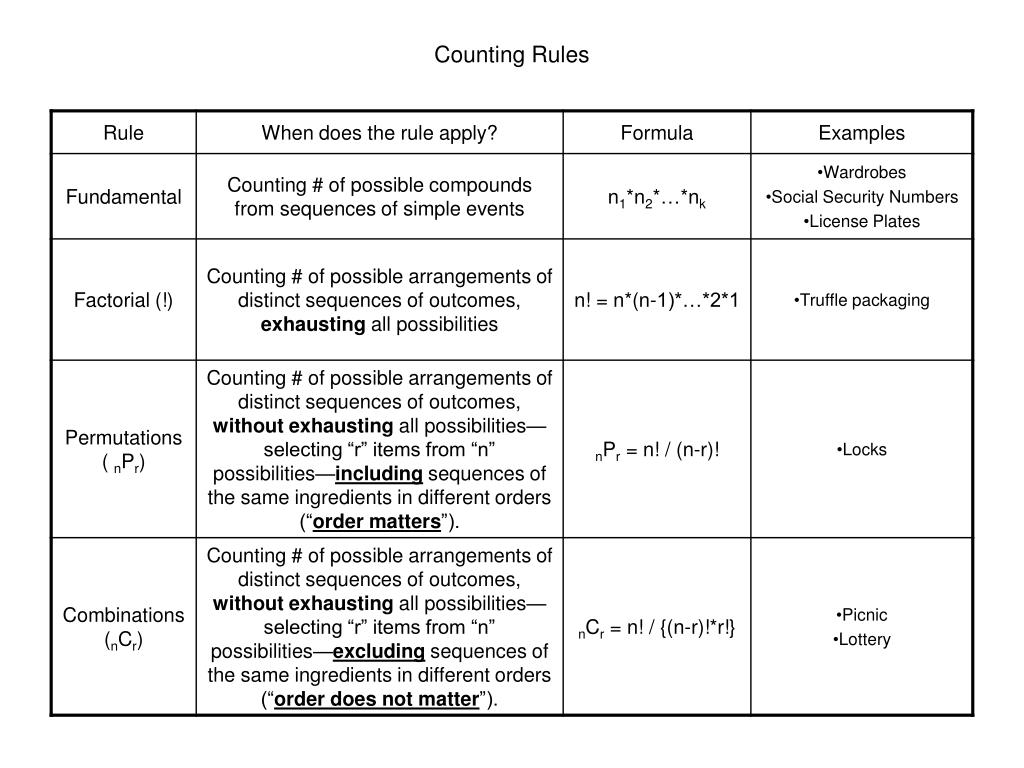
Independent probability andymath statistics
Table of Contents
Table of Contents
Do you want to learn how to calculate probability of independent events? As a fundamental concept in statistics and probability theory, understanding independent events is critical to making accurate predictions and informed decisions. In this article, we will cover the basics of independent events and how you can apply them to solve real-world problems.
When dealing with probability, there can be many pain points that arise. For example, it can be difficult to determine the likelihood of an event occurring, especially when multiple events are involved. Additionally, understanding the difference between independent and dependent events can be confusing for some learners.
Independent events occur when the outcome of one event does not affect the outcome of another. For example, if you flip a coin and roll a dice, the result of one does not affect the other. To calculate the probability of independent events, you multiply the probability of each event individually.
In summary, independent events occur when the outcome of one event does not affect the outcome of another. To calculate the probability of independent events, multiply the probability of each event. Understanding this concept is critical in many areas, including finance, insurance, and sports betting.
Why Calculate Probability of Independent Events?
One reason to learn how to calculate probability of independent events is to make more informed decisions. For example, let’s say you are a business owner and are considering investing in a new product line. By understanding the probability of certain outcomes, you can make a more informed decision about the potential return on investment. Additionally, understanding independent events is critical in many industries, including finance, insurance, and sports betting.
Real-World Example
Imagine you are a basketball coach and want to determine the probability of your team winning their next two games. The probability of winning the first game is 0.6, and the probability of winning the second game is 0.5. To calculate the probability of winning both games, you multiply the probabilities together: 0.6 * 0.5 = 0.3, or a 30% chance of winning both games.
How to Calculate Probability of Independent Events
To calculate the probability of independent events, simply multiply the probability of each event together. For example, if the probability of event A is 0.6 and the probability of event B is 0.5, the probability of both events occurring is 0.6 * 0.5 = 0.3 (or 30%).
Formula for Calculating Probability of Independent Events
P(A and B) = P(A) * P(B)
Application of Independent Events in Real Life
Understanding independent events is critical in many industries. For example, in finance, investors use probabilities to calculate the risk of certain investments. In insurance, actuarial professionals use probabilities of independent events to calculate premiums and assess risk. Additionally, sports bettors use probabilities to make informed bets on the outcome of games.
Question and Answer
Q: What is the difference between independent and dependent events?
A: Independent events occur when the outcome of one event does not affect the outcome of another. Dependent events occur when the outcome of one event affects the outcome of another.
Q: How do you calculate probability of independent events?
A: To calculate the probability of independent events, multiply the probability of each event. For example, if the probability of event A is 0.6 and the probability of event B is 0.5, the probability of both events occurring together is 0.6 * 0.5 = 0.3 (or 30%).
Q: Why is understanding independent events important?
A: Understanding independent events is critical in many areas, including finance, insurance, and sports betting. By understanding the likelihood of certain outcomes, you can make more informed decisions and mitigate risk.
Q: What is the formula for calculating the probability of independent events?
A: P(A and B) = P(A) * P(B)
Conclusion of Calculate Probability Of Independent Events
Calculating the probability of independent events is a fundamental concept in statistics and probability theory. Understanding the difference between independent and dependent events is critical in making informed decisions and mitigating risk in many industries. By applying the formula for calculating independent events, you can accurately predict the likelihood of certain outcomes and make more informed decisions.
Gallery
Dependent Probability. Dependent Probability Means The Result… | By

Photo Credit by: bing.com / probability statistical programming
Algebra 2 - 10.5 - Probabilities Of Independent And Dependent Events

Photo Credit by: bing.com / dependent independent events algebra probabilities
Independent Events - Study Material For IIT JEE | AskIITians

Photo Credit by: bing.com / independent events formula probability askiitians
Independent Events (Probability)

Photo Credit by: bing.com / independent probability andymath statistics
Independent Events (Basics Of Probability: Independence Of Two Events

Photo Credit by: bing.com / independent probability events two independence