Binomial Probability Density Function

1 3 6 6 18 binomial distribution

Table of Contents

Do you ever wonder how to predict the outcome of an experiment with only two possible outcomes? Binomial Probability Density Function might be the answer to your question.

The Pain Points of Binomial Probability Density Function

When trying to predict the outcome of an experiment, it can be difficult and time-consuming to analyze all possible outcomes. Not to mention, it can be challenging to determine the probability of each outcome. This is where Binomial Probability Density Function comes in handy.

The Target of Binomial Probability Density Function

Binomial Probability Density Function is a mathematical formula used to predict the probability of a specific number of successful outcomes in a fixed number of independent trials. Its main objective is to determine the probability distribution of a given experiment with only two possible outcomes: success or failure.

Summary of Binomial Probability Density Function’s Main Points

Binomial Probability Density Function is a mathematical formula used to predict the probability of a specific number of successful outcomes in a fixed number of independent trials with only two possible outcomes. This formula is used to calculate the probability distribution for a given experiment, saving time and effort in predicting possible outcomes.

What is Binomial Probability Density Function?

Binomial Probability Density Function is a formula that is used to calculate the probability of a certain number of successful outcomes in a fixed number of trials. This formula is used when there are only two possible outcomes for each trial: success or failure.

For example, if you are playing a game where you have a 50% chance of winning each round, Binomial Probability Density Function can help predict the number of rounds you will win out of a fixed number of total rounds.

When is Binomial Probability Density Function Used?

Binomial Probability Density Function is used in various fields, including statistics, social sciences, medical sciences, and more. It is particularly helpful in fields where experiments with only two possible outcomes are common, such as clinical trials where the success or failure of a drug’s effectiveness is being tested.

Personally, I have used Binomial Probability Density Function in analyzing the success rates of marketing campaigns. By using this formula, I was able to predict the number of successful outcomes (conversions) in a fixed number of trials (ad impressions) with only two possible outcomes: success (conversion) or failure (no conversion).

How to Use Binomial Probability Density Function

The Binomial Probability Density Function formula is:

P(x) = C(n,x) * p^x * (1-p)^(n-x)

where:

• P(x) is the probability of x successful outcomes
• C(n,x) is the number of combinations of x from n trials
• p is the probability of success for each trial
• n is the total number of trials
• x is the number of successful outcomes

Let’s say you want to calculate the probability of getting exactly 5 heads in 10 coin tosses, where the probability of getting heads is 0.5. Using the Binomial Probability Density Function formula, we get:

P(5) = C(10,5) * 0.5^5 * 0.5^(10-5)

P(5) = 252 * 0.03125 * 0.03125

P(5) = 0.24609375 or 24.61%

Benefits of Using Binomial Probability Density Function

One of the main benefits of using Binomial Probability Density Function is that it provides a quick and easy way to calculate the probability distribution of an experiment with only two possible outcomes. This can save time and effort in predicting possible outcomes and making important decisions.

Additionally, Binomial Probability Density Function is a widely used formula that can be applied in various fields, making it a valuable tool for professionals across different industries.

Question and Answer

Q: What is the difference between Binomial Probability Density Function and Binomial Distribution?

A: Binomial Probability Density Function is a formula used to calculate the probability of a certain number of successful outcomes in a fixed number of trials with only two possible outcomes. Binomial Distribution, on the other hand, is a probability distribution that shows the frequency of each possible outcome in a given experiment.

Q: How is Binomial Probability Density Function different from Poisson Distribution?

A: Binomial Probability Density Function is used for experiments with a fixed number of trials and only two possible outcomes. On the other hand, Poisson Distribution is used for experiments with a large number of trials and rare events.

Q: Can Binomial Probability Density Function be used for experiments with more than two possible outcomes?

A: No, Binomial Probability Density Function is only used for experiments with exactly two possible outcomes.

Q: What is the relationship between Binomial Probability Density Function and Standard Deviation?

A: The Standard Deviation of a Binomial Probability Density Function is calculated using the formula: sqrt(n*p*(1-p)), where n is the total number of trials and p is the probability of success for each trial.

Conclusion of Binomial Probability Density Function

Binomial Probability Density Function provides a quick and easy way to calculate the probability distribution of an experiment with only two possible outcomes. It is a valuable tool used in various fields and can save time and effort in predicting possible outcomes and making important decisions. By using the Binomial Probability Density Function formula, professionals can accurately predict the probability of a certain number of successful outcomes in a fixed number of trials, aiding in their decision-making process.

Gallery

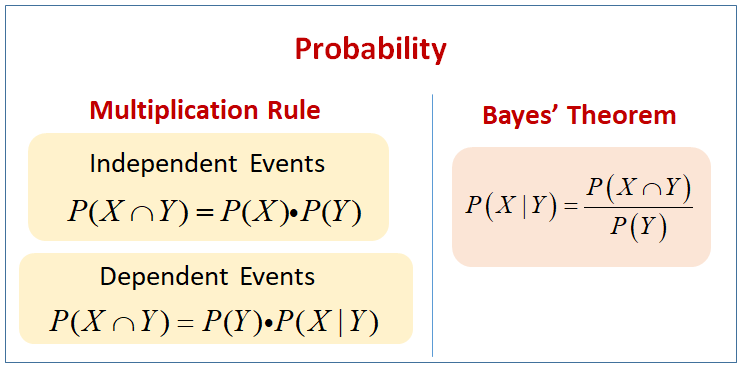
PPT - Probability And Statistics PowerPoint Presentation, Free Download

_{^{Photo Credit by: bing.com / probability binomial statistics distribution function density expectation ppt powerpoint presentation}}

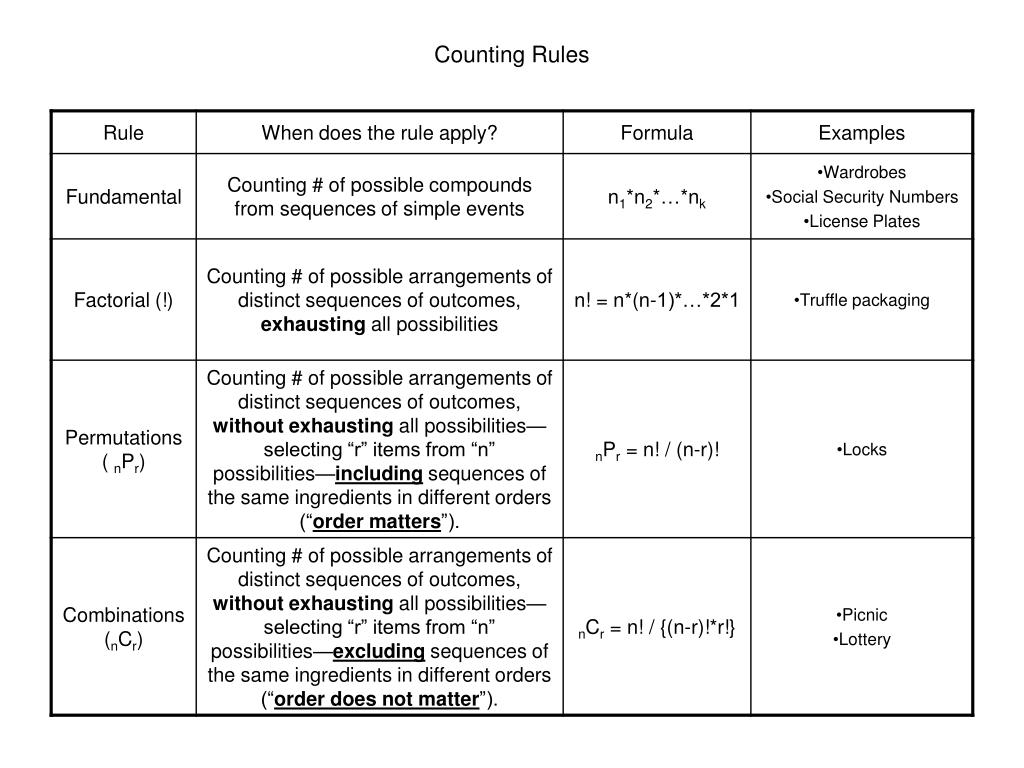
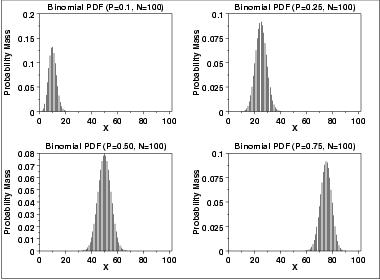
1.3.6.6.18. Binomial Distribution

_{^{Photo Credit by: bing.com / binomial probability distribution function density plot bernoulli example gif statistics descriptive science data cumulative family mass nist eda itl div898}}

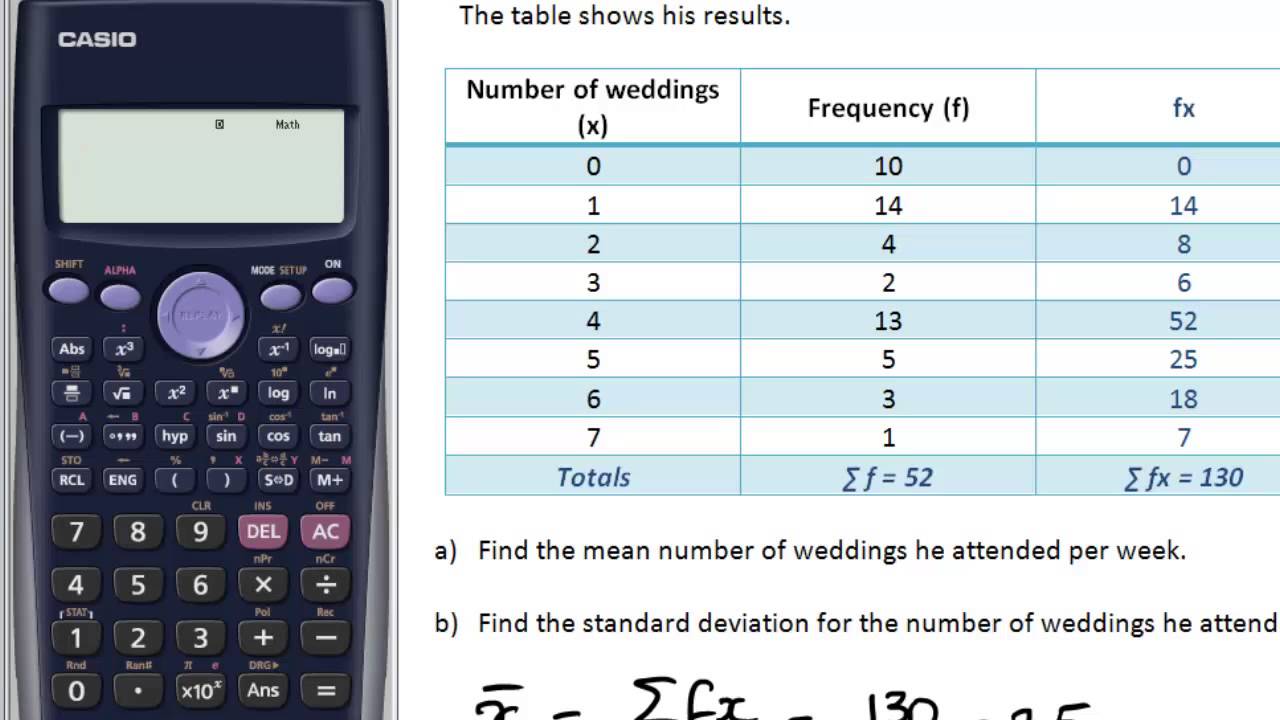
Maths For ML — Probability Distributions | By Raghunath D | Medium

_{^{Photo Credit by: bing.com / probability distribution example binomial medium}}

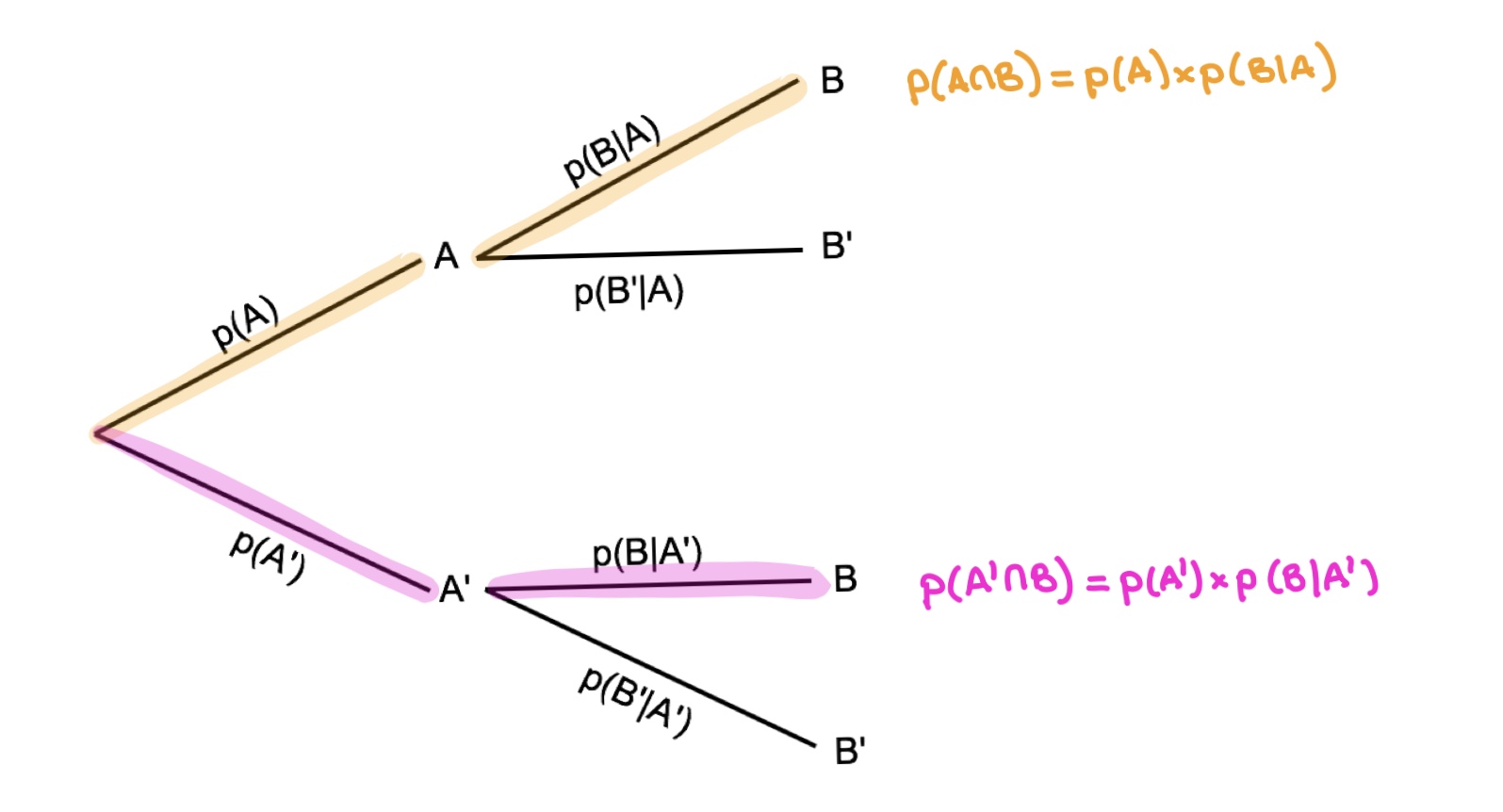
Probability (a) And Cumulative Distribution Function (b) For Binomial

_{^{Photo Credit by: bing.com / binomial cumulative probability poisson}}

PPT - Probability And Statistics PowerPoint Presentation, Free Download

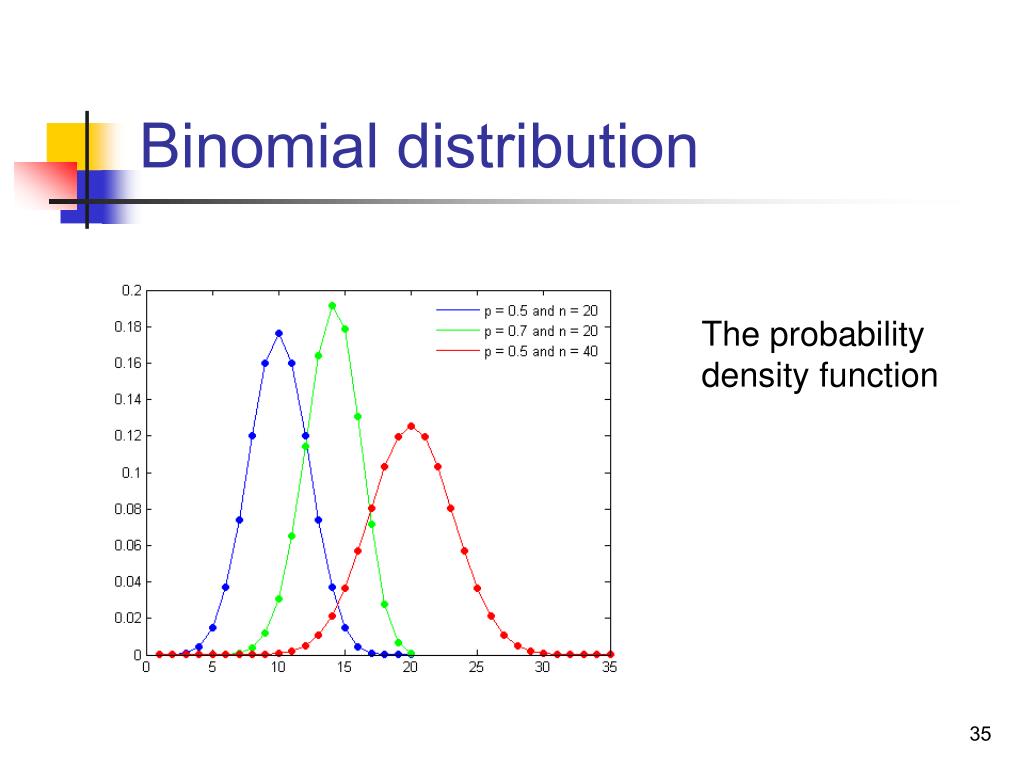
_{^{Photo Credit by: bing.com / probability binomial function distribution density statistics ppt powerpoint presentation}}