What Is Poisson Probability Distribution

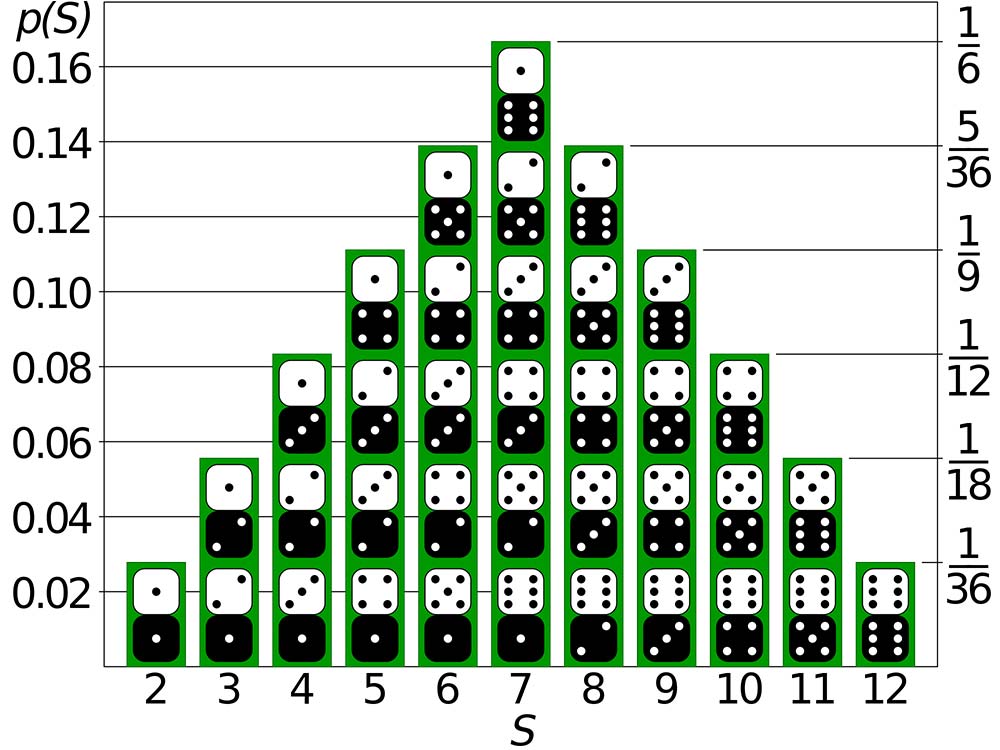
Poisson distribution probability function example variance mean statistics failures computer during applied reports manager system center his

Table of Contents

Poisson Probability Distribution is a concept used in statistics to represent the probability of a given number of events occurring in a fixed interval of time or within a specific area. It is widely used in real-world applications such as engineering, finance, biology, and many more. In this article, we will dive into the meaning and significance of Poisson Probability Distribution.

Pain Points of Poisson Probability Distribution

When it comes to analyzing data, many people are often confused by the concept of Poisson Probability Distribution. They struggle with understanding how it differs from other probability distributions, such as the Normal Distribution or Binomial Distribution. Additionally, individuals may find it challenging to calculate the distribution’s parameters or to interpret the results effectively.

What Is Poisson Probability Distribution?

Poisson Probability Distribution is a mathematical function that represents the likelihood of a specific number of events occurring within a fixed interval of time or within a specific area. This distribution is useful in situations where the number of events happening in a unit of time or area can be counted but will vary from one period to another. It is used extensively in various fields such as quality control, insurance, and biology.

Main Points of Poisson Probability Distribution

The key takeaways about Poisson Probability Distribution are as follows:

• It represents the probability of a given number of events occurring in a fixed interval of time or area.
• It is useful when the events occur randomly, but the average rate of occurrence is known.
• It is often used to model real-life events such as accidents, customer arrivals, and the number of defects in a production line.
• The formula for Poisson Probability Distribution involves two parameters - the average rate of occurrence and the number of events in question.

Understanding the Formula and Parameters of Poisson Probability Distribution

To understand the Poisson Probability Distribution formula, we must first know the two parameters used - mean or average rate of occurrence and the number of events in question. The probability of a given number of events occurring in a set interval can be calculated using the following formula:

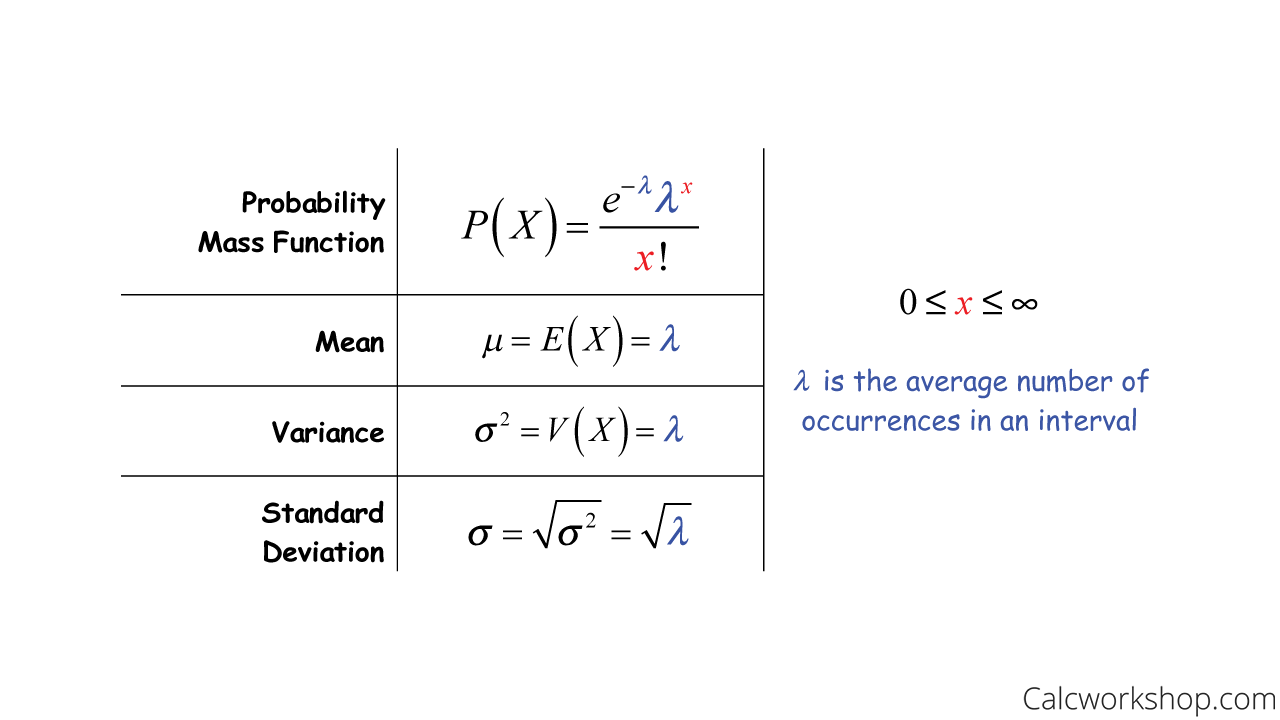Where;

• e is the mathematical constant with a value of 2.71828
• μ is the mean or average rate of occurrence
• k is the total number of events
• k! is the factorial of k

This formula is used to determine the probability of a particular number of events occurring within a specific interval of time while assuming that these events are randomly and independently distributed.

Applications of Poisson Probability Distribution

Poisson Probability Distribution finds its use in several industries to make decisions and forecasts. A few of these instances that use the distribution are -

• In insurance, the distribution can help estimate the rate of claims that are expected on any given day.
• In the manufacturing industry, it is used to analyze the number of defects in a particular production line.
• The analysis of website traffic, finding the number of mail arriving at local post offices can be done using Poisson Probability Distribution.

Tips for Understanding Poisson Probability Distribution

To better understand Poisson Probability Distribution, consider the following tips:

• Understand the significance of each of the distribution’s parameters - mean or average rate of occurrence and the number of events in question.
• Familiarize yourself with the Poisson Probability Distribution formula.
• Utilize resources such as online tutorials, textbooks, and software packages to aid in understanding the concept.

Question and Answer

Question 1: What is Poisson Probability Distribution used for?

Answer: Poisson Probability Distribution is used in various fields such as quality control, insurance, and biology, to represent the probability of a specific number of events occurring within a fixed interval of time or area.

Question 2: What are the parameters of Poisson Probability Distribution?

Answer: The two parameters in Poisson Probability Distribution are the mean or average rate of occurrence and the number of events in question.

Question 3: How is Poisson Probability Distribution formula calculated?

Answer: Poisson Probability Distribution formula is calculated using the mean or average rate of occurrence and the total number of events and follows the formula as:

P(X=k)= (e^-μ)* (μ^k)/k!

Question 4: What are the real-life applications of Poisson Probability Distribution?

Answer: Poisson Probability Distribution finds its use in several industries to make decisions and forecasts. A few of these instances that use the distribution are website traffic analysis, mail arriving at local post offices, and finding the number of defects in a production line.

Conclusion of What Is Poisson Probability Distribution

Poisson Probability Distribution is a valuable tool in statistical analysis that helps represent the probability of a specific number of events occurring within a fixed interval of time or an area. The formula for Poisson Probability Distribution is straightforward, and with some practice, one can easily use it in different industries to make decisions and forecasts. As with any statistical tool, a thorough understanding of its application and formula is essential in effectively utilizing Poisson Probability Distribution to make informed decisions.

Gallery

Poisson Distribution

_{^{Photo Credit by: bing.com / poisson andymath}}

Variance Of Probability Distribution Formula - Research Topics

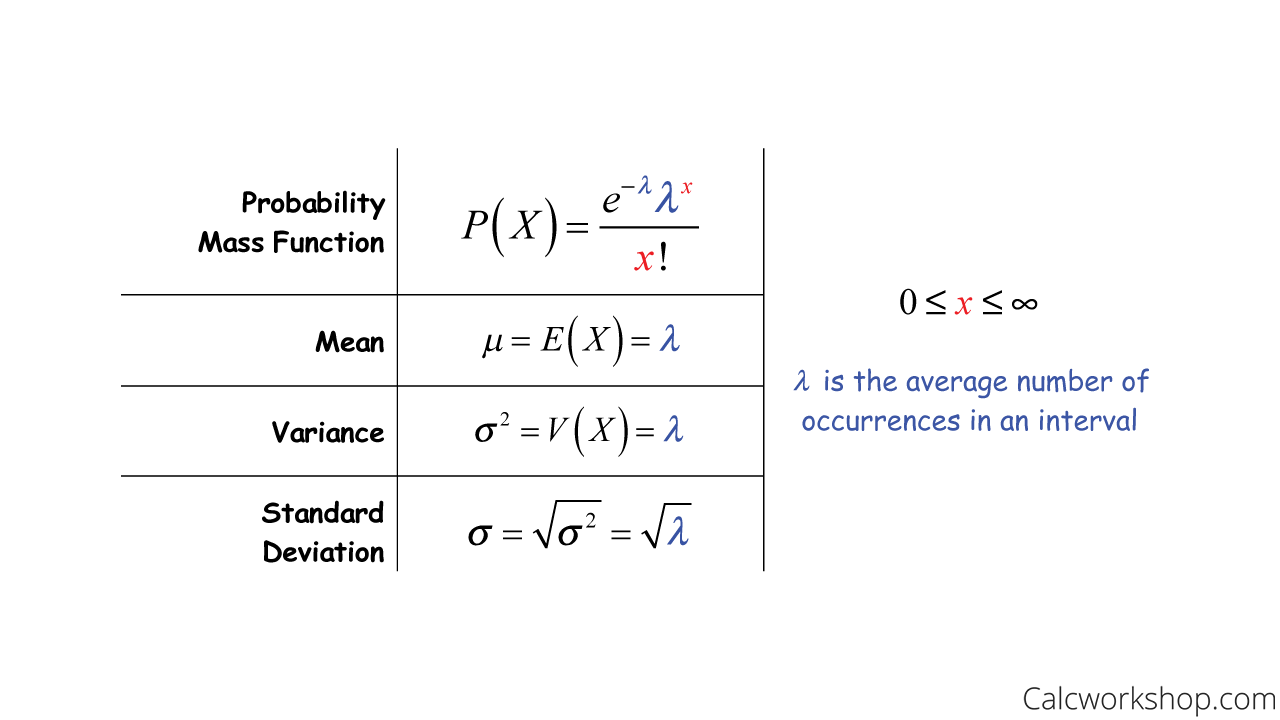
_{^{Photo Credit by: bing.com / variance poisson probability examples pmf stat}}

Poisson Distribution | Psychology Wiki | FANDOM Powered By Wikia

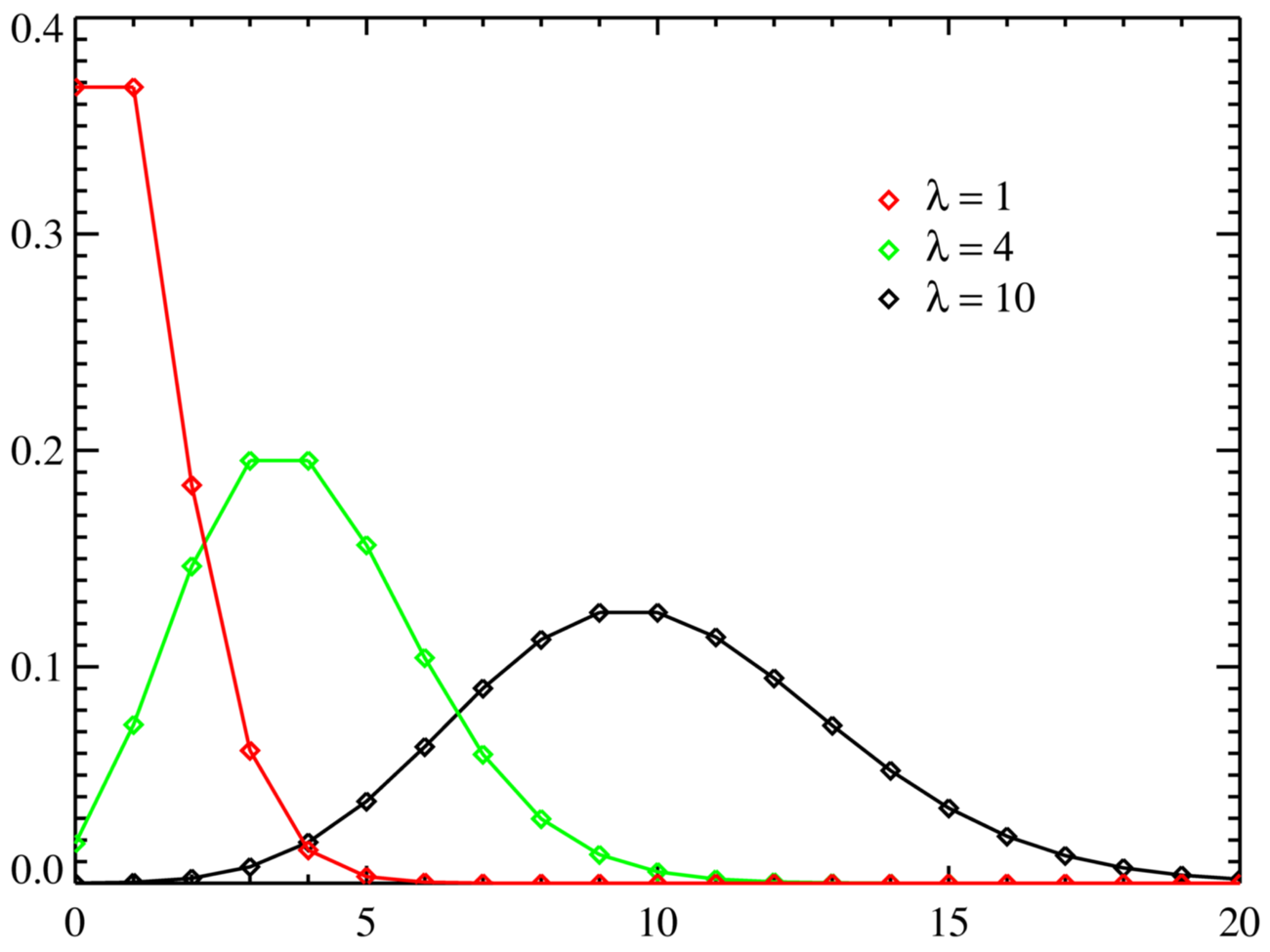
_{^{Photo Credit by: bing.com / poisson distribution}}

Probability Distribution- Poisson - From The GENESIS

_{^{Photo Credit by: bing.com / poisson distribution probability histogram log fit given}}

Applied Statistics: The Poisson Probability Distribution Function, Mean

_{^{Photo Credit by: bing.com / poisson distribution probability function example variance mean statistics failures computer during applied reports manager system center his}}