Probability discrete
Table of Contents
Table of Contents
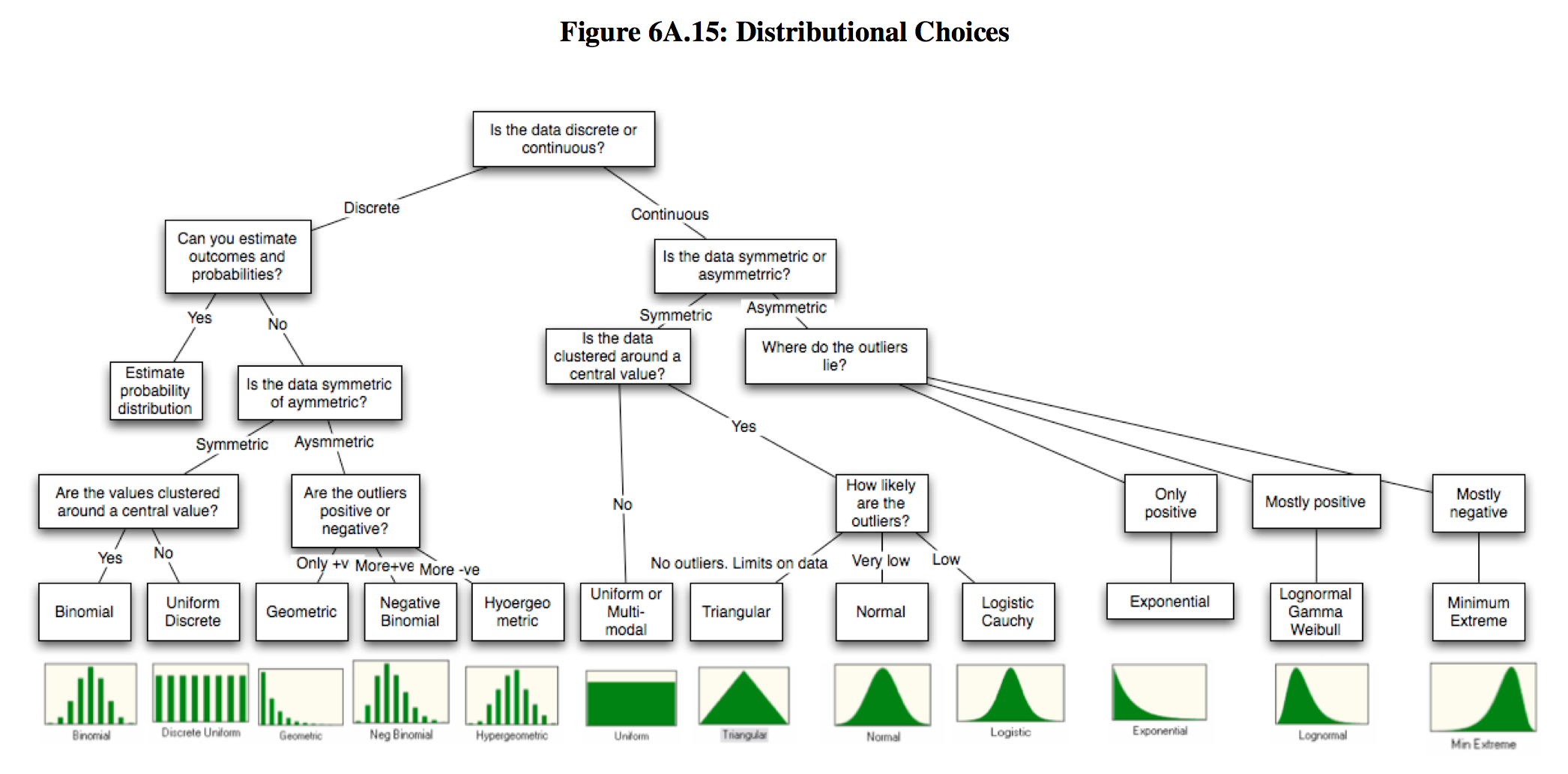
Have you ever wondered about the different types of discrete probability distributions and their characteristics? Understanding these concepts can have a significant impact on data analysis and decision-making. In this article, we will explore the various types of discrete probability distributions and their applications.
Pain Points
When dealing with data, one of the main challenges is identifying the probability distribution underlying the data. Discrete probability distributions can have different characteristics, which impacts how we analyze and interpret the data. Therefore, understanding the different types of discrete probability distributions is crucial in data analysis, modeling, and decision-making processes.
Target of Discrete Probability Distributions
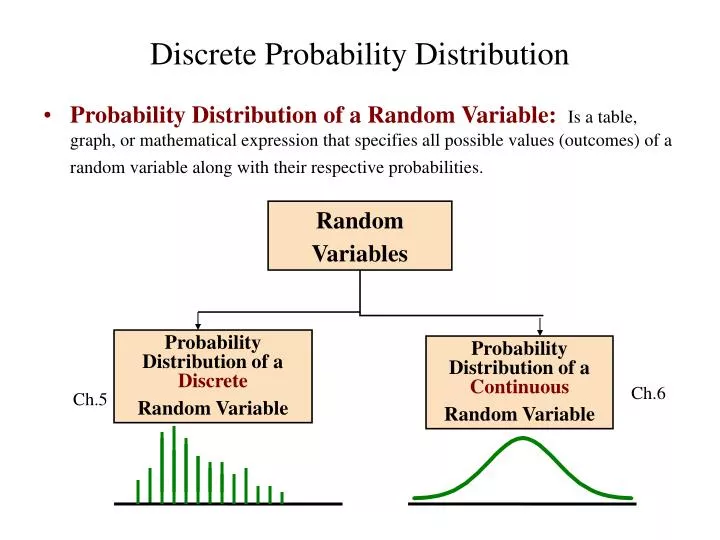
Discrete probability distributions are used to model random variables that take on a discrete number of values. These distributions define the probability of each value occurring and provide insight into the characteristics of the data. Understanding these distributions helps in making decisions about the data and the underlying process generating the data.
Summary of the Main Points
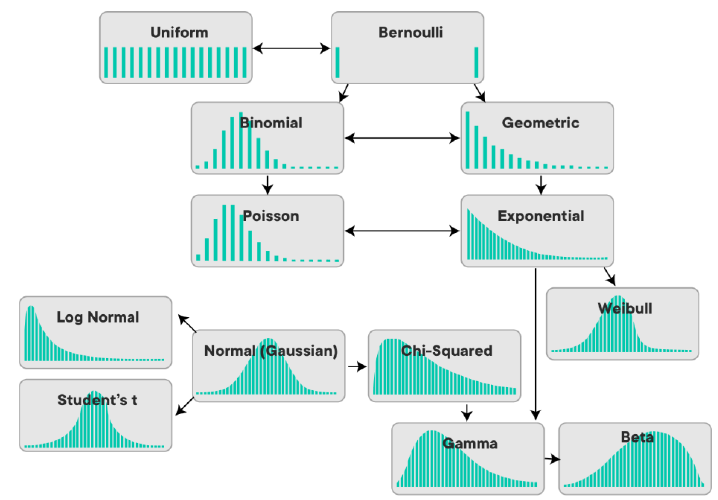
We explored the various types of discrete probability distributions, their characteristics, and applications. They include the binomial distribution, Poisson distribution, geometric distribution, and hypergeometric distribution. Understanding these distributions is crucial in data analysis and modeling, and it helps in making sound business decisions.
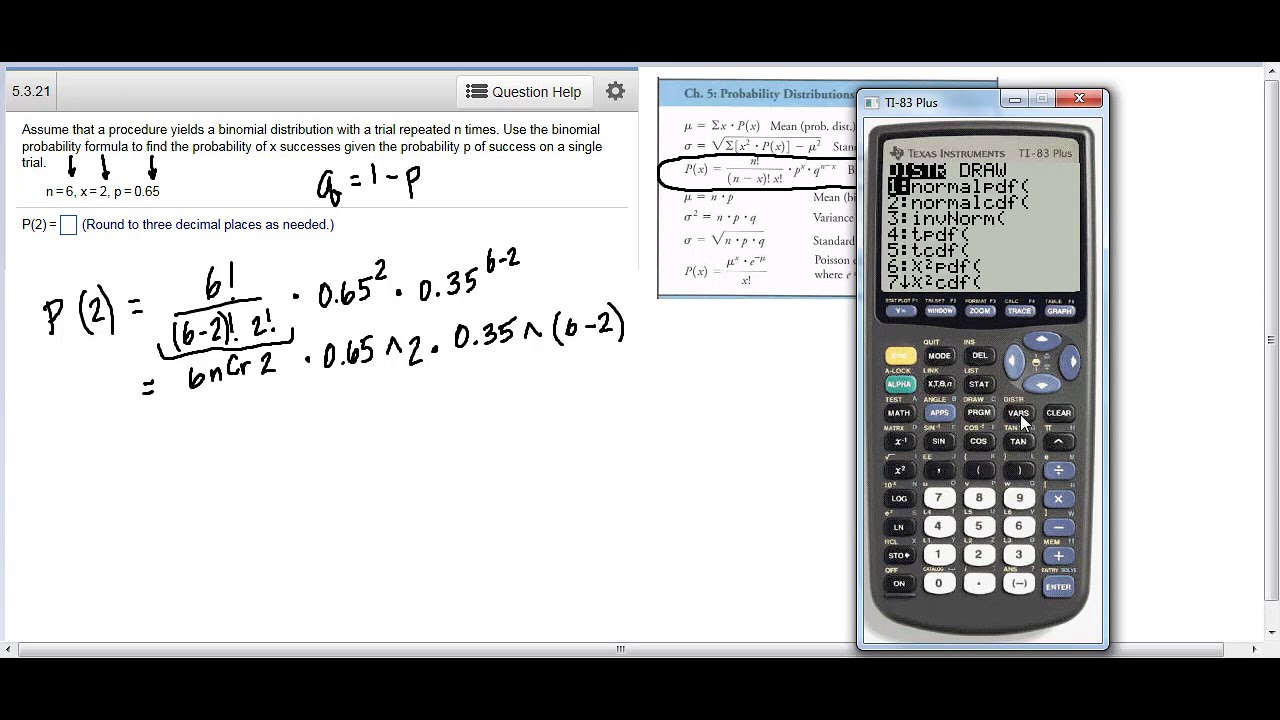
Binomial Distribution
The binomial distribution is a statistical distribution that describes the number of successes in a fixed number of trials. Let’s say you conduct a series of coin tosses. The binomial distribution enables you to calculate the probability of getting “x” number of heads in “n” number of coin tosses. The binomial distribution has two parameters: “n” and “p”.
For example, if you flip a coin ten times (n=10), the probability of getting four heads (x=4) is 0.205. The binomial distribution is widely used in quality control, opinion polls, and marketing research.
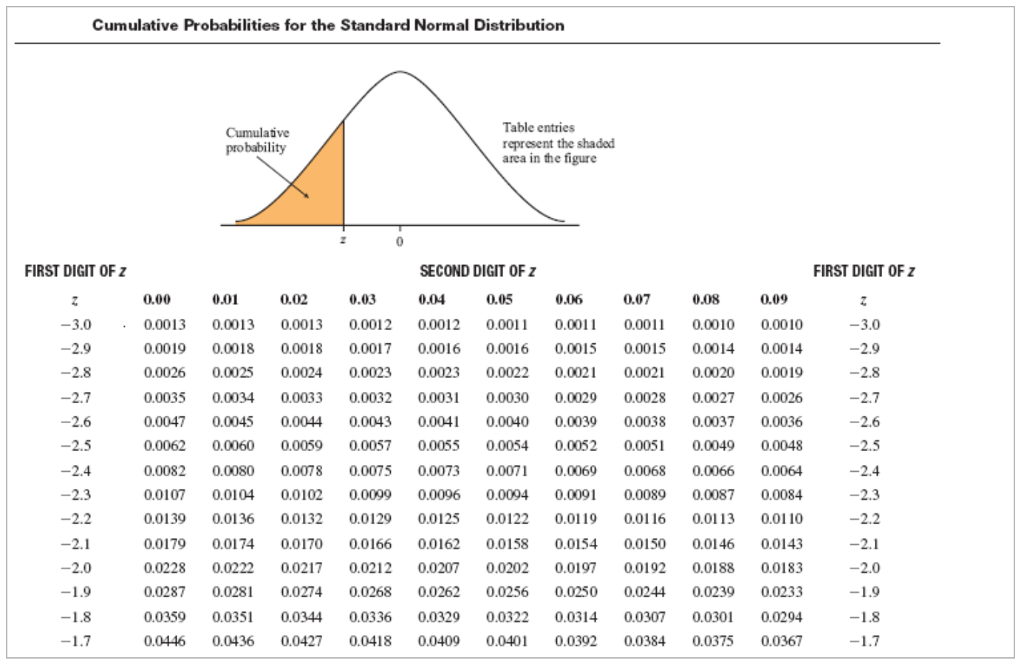
Poisson Distribution
The Poisson distribution is used to describe the number of events occurring in a fixed interval of time or space. It is a discrete distribution that has one parameter, “lambda”, which represents the expected number of events in the interval.
For example, the Poisson distribution can be used to model the number of calls received by a call center within a particular time. By knowing the average number of calls per hour, we can determine the probability of receiving a certain number of calls in an hour using the Poisson distribution. Other applications of the Poisson distribution include insurance claims, traffic accidents, and medical research.
Geometric Distribution
The geometric distribution describes the number of independent and identically distributed (i.i.d) Bernoulli trials needed to obtain the first success. It has one parameter “p”, which represents the probability of success in each trial.
For example, the geometric distribution can be used to model the number of attempts it takes to win a game of chance or the number of attempts needed to get a defective product. The geometric distribution can also be used to study patterns of user behavior on websites or social media platforms.
Hypergeometric Distribution
The hypergeometric distribution describes the probability of obtaining a certain number of successes in a sample without replacement. It is used to model situations where the sample size is small compared to the population size.
For example, the hypergeometric distribution can be used to determine the probability of selecting a particular number of defective products from a small batch of items in a quality control process.
Question and Answer
Q: What is the difference between the Poisson and binomial distribution?
A: The Poisson distribution is used to model the number of events occurring in a fixed interval, whereas the binomial distribution models the number of successes in a fixed number of trials.
Q: What is the target application of the geometric distribution?
A: The geometric distribution can be used to model the number of independent and identically distributed Bernoulli trials needed to obtain the first success.
Q: What are the parameters of the hypergeometric distribution?
A: The hypergeometric distribution has three parameters: “N”, which is the population size, “n”, which is the sample size, and “k”, which is the number of successes in the population.
Q: What is the application of the hypergeometric distribution?
A: The hypergeometric distribution is used to model situations where the sample size is small compared to the population size, such as in quality control processes or medical research.
Conclusion of Types Of Discrete Probability Distributions
Discrete probability distributions play a fundamental role in data analysis, modeling, and decision-making processes. In this article, we explored the different types of discrete probability distributions, their characteristics, and their applications. The binomial distribution, Poisson distribution, geometric distribution, and hypergeometric distribution are some of the most commonly used probability distributions. Understanding these distributions can help in making sound business decisions and in acquiring valuable insights from data analysis.
Gallery
Application Of Probability Distribution In Real Life Ppt - Research Topics
Photo Credit by: bing.com / probability discrete
Statistics In Marketing - Discrete Probability Distributions | Bernard-ML
Photo Credit by: bing.com / probability distributions discrete
Probability Distributions And Their Mass/Density Functions
Photo Credit by: bing.com / probability continuous functions distributions density probabilistic distr prob approaches
9 Common Probability Distributions With Mean & Variance Derivations
Photo Credit by: bing.com / probability variance distributions function derivations cumulative
Different Types Of Probability Distribution (Characteristics & Examples
Photo Credit by: bing.com / probability types statistics characteristics distributions poisson binomial
