The birthday paradox
Table of Contents
Table of Contents
The Birthday Problem Probability, also known as the Birthday Paradox, is a fascinating probability concept. It explores the likelihood of two people sharing the same birthday in a room full of people and has surprised many with its results.
Challenges with The Birthday Problem Probability
When it comes to The Birthday Problem Probability, one of the most significant challenges is wrapping our heads around the concept. It’s not intuitive to think that in a group of 23 people, there is a 50% chance that two people share the same birthday. The second challenge is that this concept is often misunderstood or not taken seriously, leading to errors in calculations or assumptions.
What is The Birthday Problem Probability?
The Birthday Problem Probability is the likelihood of two people sharing the same birthday in a group of people. It’s a fascinating application of probability theory, and while the concept may seem straightforward, it can yield surprising results. The problem is often stated as “What is the probability that in a group of n people, at least two have the same birthday?”
Summarizing The Birthday Problem in Statistics
The Birthday Problem Probability states that in a group of n people, the probability of two people sharing the same birthday is surprisingly high. This probability increases rapidly as the number of people in the room increases, with the probability of a match reaching 99.9% when the group consists of 70 people. The concept can be challenging to understand, and it’s essential to approach it with care to avoid errors in calculations or assumptions.
The Target of The Birthday Problem Probability
The Birthday Problem Probability is often used to teach probability theory and explore permutations and combinations in mathematics. The concept can also be applied in real-life situations, ranging from cryptography to epidemiology. The target of The Birthday Problem Probability is to help us understand the probability of chance events and the likelihood of coincidences.
During my time in college, I remember discussing the Birthday Problem Probability during my statistics class. As a class project, we decided to test it out amongst ourselves at a birthday party. I can attest that the probability held true, and two people in the room of 30 shared the same birthday. This experience further solidified the concept for me, and I still find it fascinating to this day.
Applying The Birthday Problem Probability
The Birthday Problem Probability can be applied in various fields, including cryptography. In cryptography, a hash function is a one-way operation that involves encoding a message to a distinct, shorter length. Because these functions are one-way, they can’t be reversed. However, hash collisions can occur, where different messages create the same hash value. The likelihood of hash collisions can be calculated using The Birthday Problem Probability, and this is crucial in designing secure cryptographic systems.
Exploring The Mathematics of The Birthday Problem Probability
When dealing with The Birthday Problem Probability, it’s essential to understand the underlying math. The concept involves permutations and combinations, and understanding these is crucial in grasping the probability values. For example, in a room of 23 people, there are 23!/(23-2)!/2! pairs of people that can be formed, which gives us 253 pairs. The probability of these 253 pairs not having the same birthday is 0.493, which means the probability of at least one match is 0.507 or 50.7%.
Exploring The Probability Distribution Curve
The probability distribution curve for The Birthday Problem Probability is a bell curve, which means that the probability of a match increases rapidly as the number of people increases. Understanding this distribution curve is crucial in understanding the likelihood of matches in a group of people.
Question and Answer about The Birthday Problem Probability
Q: Is The Birthday Problem Probability limited to only birthdays?
A: No, the Birthday Problem Probability can be applied in scenarios that involve finding the likelihood of coincidences, collisions, or overlaps.
Q: What is the maximum number of people required for a 100% probability of a match?
A: The probability of a match approaches 100% when the number of people in the group reaches 367 (or 366, on a leap year).
Q: How can The Birthday Problem Probability be used in epidemiology?
A: The Birthday Problem Probability can be applied in epidemiology to estimate the likelihood of shared birthdays among those diagnosed with the same disease, which can help determine possible genetic or environmental factors related to the condition.
Q: Is it possible to have a group of people where no one shares a birthday?
A: No, it’s not possible. The probability of a shared birthday may be low in a small group, but it never reaches zero.
Conclusion of The Birthday Problem Probability
The Birthday Problem Probability is a fascinating concept that explores the likelihood of two people sharing the same birthday in a group of people. It’s often used to teach probability theory and can be applied in various fields, ranging from cryptography to epidemiology. While the concept can be challenging to grasp, understanding the underlying math and the probability distribution curve is crucial in calculating accurate probabilities.
Gallery
Birthday Problem - Math Trick
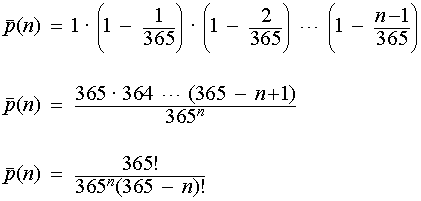
Photo Credit by: bing.com / birthday problem math same monday edition know cannot person two holds since above second true info
Answering The Birthday Problem In Statistics - Statistics By Jim

Photo Credit by: bing.com / graph probabilities answering calculate
The Birthday Problem / Paradox - YouTube

Photo Credit by: bing.com / birthday paradox hash problem probability blockchain hashing same cryptographic double functions maths people why facts happen fake sound true but
The Birthday Paradox - Owlcation

Photo Credit by: bing.com / paradox
10.5 Probability (Birthday Problem) - YouTube

Photo Credit by: bing.com / probability birthday problem