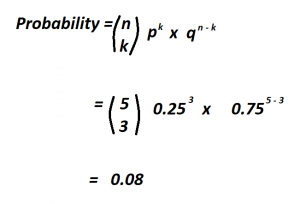Binomial distribution probability mean variance ppt success standard deviation cdf trials powerpoint presentation
Table of Contents
Table of Contents
The Binomial Probability Distribution is an essential concept in probability theory that helps calculate the probability of a specific number of successes in a sequence of independent trials. Understanding this concept is crucial for statisticians, data analysts, and anyone looking to make informed decisions based on data. In this blog post, we explore The Binomial Probability Distribution, its applications, and how it works.
Pain Points related to The Binomial Probability Distribution
Working with probability distributions can be challenging, even for experienced statisticians. It can be challenging for people who are not familiar with the notation and the concepts of probability theory to understand how these distributions work and how to apply them to real-world problems.
What is The Binomial Probability Distribution?
The Binomial Probability Distribution represents the probability distribution for the number of successes in a fixed number of independent trials, where each trial has a constant probability of success. The distribution is defined by two parameters: n, the number of trials, and p, the probability of success in each trial. The probability of getting exactly k successes in n trials, where the probability of success in each trial is p, can be calculated using the following formula:
The Binomial Probability Distribution is widely used in many fields, including medical trials, market research, and quality control in manufacturing. It is also used in hypothesis testing, where the null and alternative hypotheses involve counting the number of successes in a fixed number of trials.
Target and Explanation
The target of The Binomial Probability Distribution is to calculate the probability of a specific number of successes in a sequence of independent trials. Let’s take the example of flipping a coin. The probability of getting heads on any given flip is 0.5, assuming the coin is fair. If we flip the coin ten times, what is the probability of getting exactly six heads?
The answer to this question involves using the Binomial Probability Distribution formula. We can calculate the probability of getting exactly six heads in ten flips using the Binomial Probability formula, which gives us a probability of approximately 0.205. This means that if we were to repeat the ten coin flips many times, we would expect to get exactly six heads approximately 20% of the time.
Applications of The Binomial Probability Distribution
The Binomial Probability Distribution has numerous applications in many fields. For example, in market research, the distribution can be used to determine the probability of a specific outcome based on a survey sample. In manufacturing, the distribution can be used to determine the probability of a specific number of defective parts in a batch. In finance, the distribution can be used to determine the probability of a specific number of profitable trades in a series of trades.
How does The Binomial Probability Distribution work?
The Binomial Probability Distribution works by calculating the probability of a specific number of successes in n independent trials, where each trial has a constant probability of success. The formula for calculating this probability involves the values of n, p, and k, where n is the number of trials, p is the probability of success in each trial, and k is the number of successes. The formula for calculating the probability of k successes in n trials is as follows:
Using this formula, we can calculate the exact probability of getting k successes in n trials. This probability can be used to make informed decisions and to perform hypothesis testing.
Real-world Example
Let’s take the example of a factory that produces light bulbs. Each bulb has a 95% chance of working correctly. A sample of 100 bulbs is selected from a batch. What is the probability that exactly 90 bulbs work correctly?
To solve this problem, we can use the Binomial Probability Distribution formula, which gives us the probability of getting exactly 90 working bulbs out of 100. Using the formula, we get a probability of approximately 0.013, which means that the probability of randomly selecting 100 bulbs from the batch and getting exactly 90 working bulbs is about 1.3%.
Question and Answer
Q1. What is the Binomial Probability Distribution used for?
The Binomial Probability Distribution is used to calculate the probability of a specific number of successes in a sequence of independent trials, where each trial has a constant probability of success. It has numerous applications in fields such as market research, manufacturing, and finance.
Q2. What are the two parameters of The Binomial Probability Distribution?
The two parameters of The Binomial Probability Distribution are n, the number of trials, and p, the probability of success in each trial.
Q3. What is the formula for The Binomial Probability Distribution?
The formula for The Binomial Probability Distribution is as follows: P(X=k) = (n choose k) * p^k * (1-p)^(n-k), where P(X=k) is the probability of getting exactly k successes in n trials, p is the probability of success in each trial, and (n choose k) is the binomial coefficient.
Q4. What is the target of The Binomial Probability Distribution?
The target of The Binomial Probability Distribution is to calculate the probability of a specific number of successes in a sequence of independent trials.
Conclusion of The Binomial Probability Distribution
The Binomial Probability Distribution is an essential concept in probability theory that helps calculate the probability of a specific number of successes in a sequence of independent trials. It has numerous applications in many fields and is used to make informed decisions based on data. Understanding this concept is crucial for statisticians, data analysts, and anyone looking to make data-driven decisions.
Gallery
Binomial Probability Distribution Tutorial
Photo Credit by: bing.com / binomial probability formulas calculate successes onlinemathlearning trials tosses fraction bernoulli roll
PPT - Binomial Probability Distribution 1. The Experiment Must Have A
Photo Credit by: bing.com / binomial probability distribution formula experiment trials fixed number method must ppt powerpoint presentation qn px slideserve
Binomial Probability Distribution - Data Science Kernel
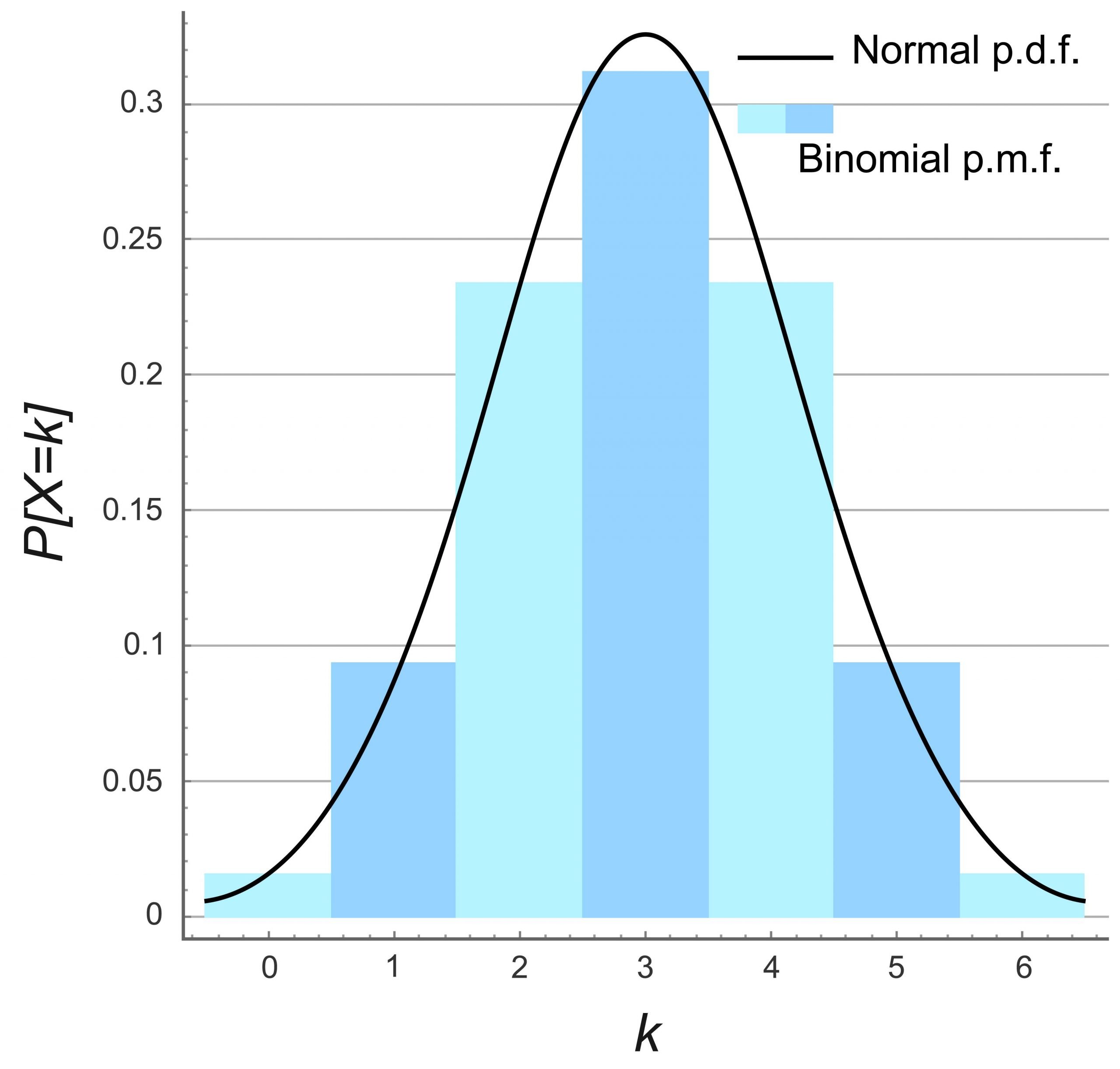
Photo Credit by: bing.com / distribution binomial probability statistics
Bernoulli Random Variables And The Binomial Distribution In Probability
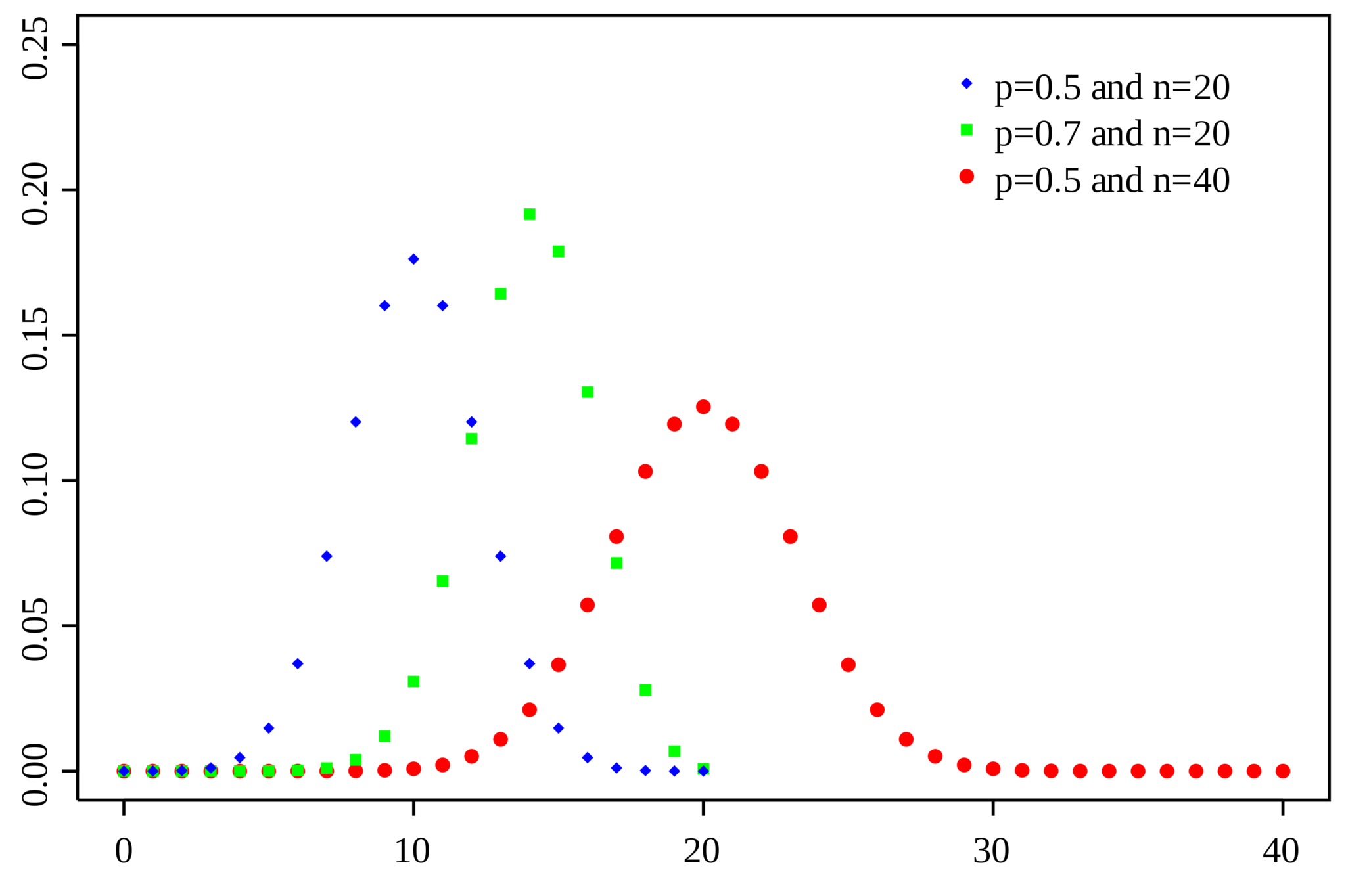
Photo Credit by: bing.com / binomial bernoulli normal probability binomiale distribuzione variance pmf binomialverteilung variables discreta plot parameter
PPT - Binomial Probability Distribution PowerPoint Presentation, Free
Photo Credit by: bing.com / binomial distribution probability mean variance ppt success standard deviation cdf trials powerpoint presentation
