Probabilities probability generating
Table of Contents
Table of Contents
If you’re studying statistics, you’ve probably heard of Table A Standard Normal Probabilities. This table is a valuable tool for anyone working with normal distributions, but it can be overwhelming to understand at first. In this article, we’ll dive into Table A Standard Normal Probabilities, its uses, and how to interpret it.
If you’ve ever worked with normal distributions, you know that they can be complicated. Even if you understand the basics, there are plenty of nuances that can trip you up. That’s where Table A Standard Normal Probabilities comes in. This table makes it easy to find the probability of a given z-score in a normal distribution. However, figuring out how to use the table can be a pain point for many students.
The main target of Table A Standard Normal Probabilities is to provide an easy way to find the probability for a given z-score in a normal distribution. This can be helpful for a variety of applications, from calculating probabilities in scientific experiments to predicting stock prices.
To summarize, Table A Standard Normal Probabilities is a valuable tool for anyone working with normal distributions. It helps you find the probability of a given z-score quickly and easily, making it an essential resource for statisticians and researchers.
What is Table A Standard Normal Probabilities?
Table A Standard Normal Probabilities is a table that shows the probability of a given z-score in a normal distribution. The table lists z-scores from -3.99 to 3.99 in increments of .01, along with their corresponding probabilities. You can use this table to find the probability of a z-score in a normal distribution without having to calculate it manually, which can save you a lot of time and effort.
When I was first learning about Table A Standard Normal Probabilities, I struggled to understand how to use it. However, once I started using it regularly, I found that it became second nature. One tip that helped me was to focus on the row and column headers. The row headers list the first two digits of the z-score, while the column headers list the third digit. By combining the row and column headers, you can quickly find the probability of a given z-score.
How to Use Table A Standard Normal Probabilities
To use Table A Standard Normal Probabilities, you first need to find the z-score that corresponds to the value you’re interested in. Once you have the z-score, you can use the table to find the probability. Here’s an example:
Suppose you want to find the probability of getting a z-score of -1.5 in a normal distribution. First, you would locate the row that corresponds to a z-score of -1.5, which is the row that starts with -1.5. Then, you would find the column that corresponds to .00, which is the column that starts with .0. The value at the intersection of these rows and columns is .0668, which is the probability of getting a z-score of -1.5 in a normal distribution.
How is Table A Standard Normal Probabilities Helpful?
One of the biggest benefits of Table A Standard Normal Probabilities is that it makes it easy to calculate probabilities in a normal distribution without having to do any complex calculations. This can save statisticians and researchers a lot of time and effort, and it can also help prevent errors. By using the table, you can quickly find the probability of a given z-score, which can be incredibly helpful in a variety of applications.
Limitations of Table A Standard Normal Probabilities
While Table A Standard Normal Probabilities is a powerful tool, it does have some limitations. For one thing, it only works for standard normal distributions, which means distributions with a mean of 0 and a standard deviation of 1. Additionally, the table only goes up to a z-score of 3.99, which means that it may not be helpful for extremely large or small z-scores.
FAQs About Table A Standard Normal Probabilities
Q: What is a z-score?
A: A z-score is a measure of how many standard deviations a data point is from the mean in a normal distribution.
Q: How do you find the probability of a given z-score?
A: You can use Table A Standard Normal Probabilities to find the probability of a given z-score. Simply locate the row and column that correspond to your z-score and read the probability at the intersection of those rows and columns.
Q: What is a standard normal distribution?
A: A standard normal distribution is a specific type of normal distribution with a mean of 0 and a standard deviation of 1.
Q: How accurate is Table A Standard Normal Probabilities?
A: Table A Standard Normal Probabilities is very accurate, as long as you’re working with a standard normal distribution. However, if you’re working with a distribution that deviates significantly from a standard normal distribution, the table may not be as helpful.
Conclusion of Table A Standard Normal Probabilities
Table A Standard Normal Probabilities is a powerful tool for anyone working with normal distributions. It makes it easy to find the probability of a given z-score quickly and accurately, which can be incredibly helpful in a variety of applications. While the table has some limitations, it’s still an essential resource for statisticians and researchers.
Gallery
Use The Standard Normal Table To Find The Z-score That Correspondents
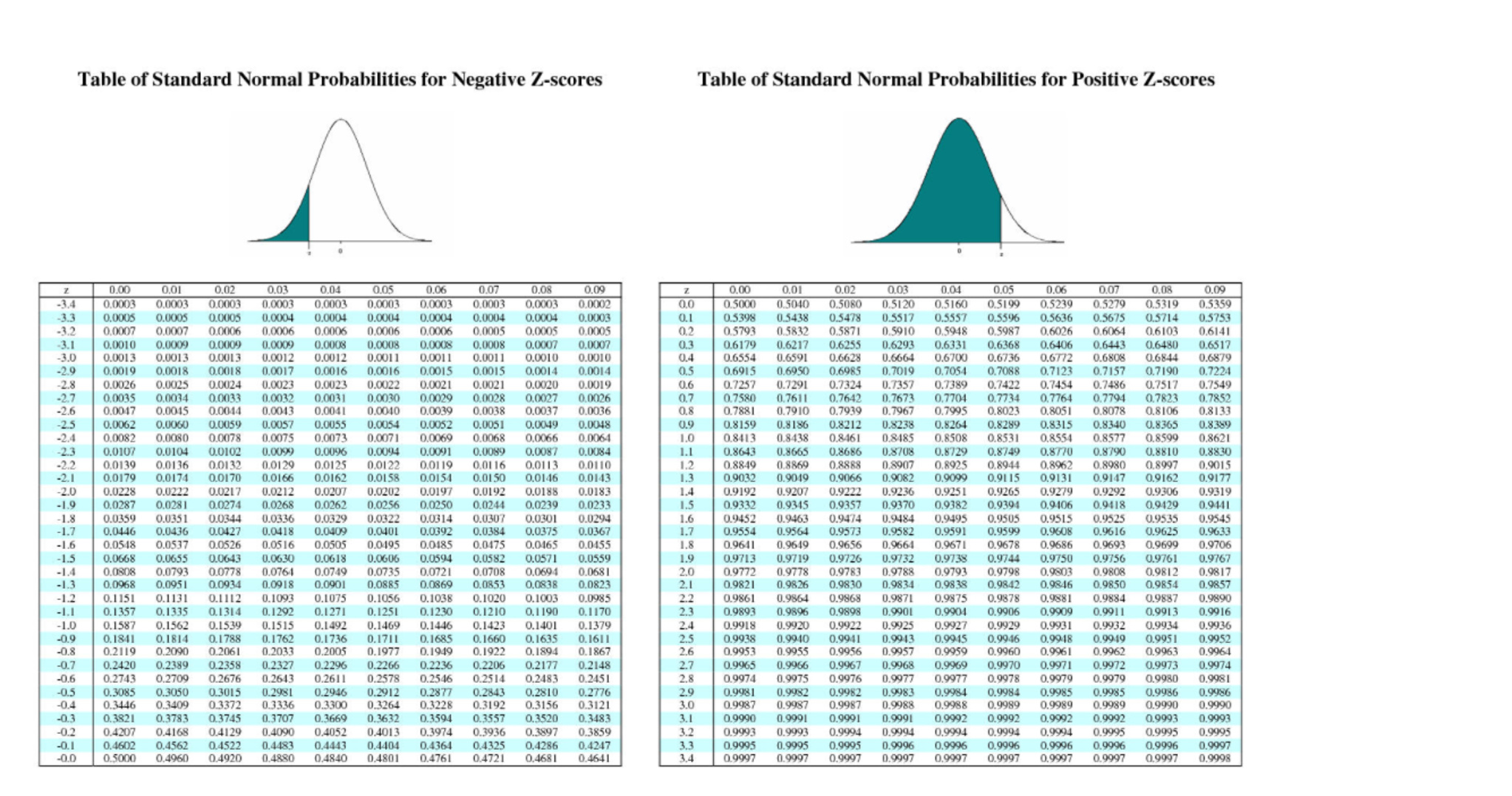
Photo Credit by: bing.com / score normal table standard find percentile cumulative area use given corresponds areas negative positive scores probabilities curve under if p4
Solved Probability Table Entry For Z Is The Area Under The | Chegg.com
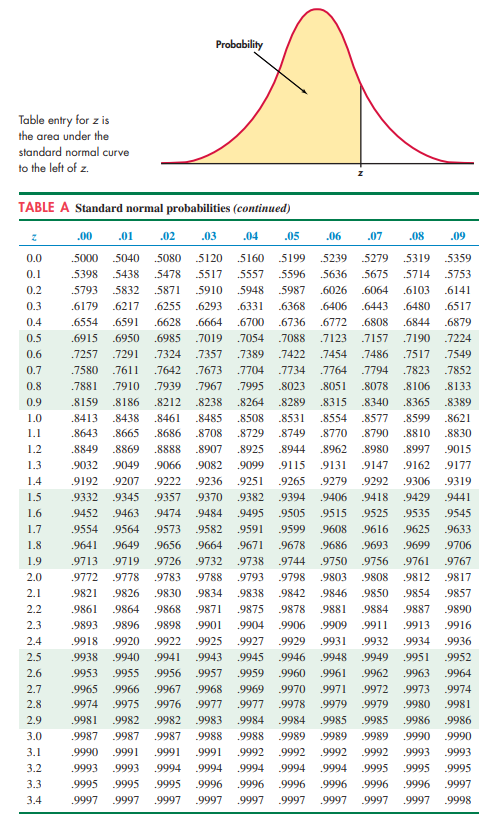
Photo Credit by: bing.com / table probability normal left standard area curve under entry solved
Normal Probability Distribution Table Pdf | Brokeasshome.com
.jpg)
Photo Credit by: bing.com / probabilities probability generating
Normal Probabilities From A Table With Negative Z’s – GeoGebra
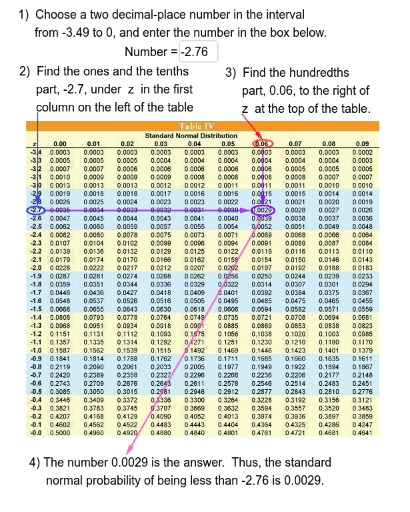
Photo Credit by: bing.com / normal probability geogebra probabilities
Solved: Cumulative Probabilities For The Standard Normal D… | Chegg.com
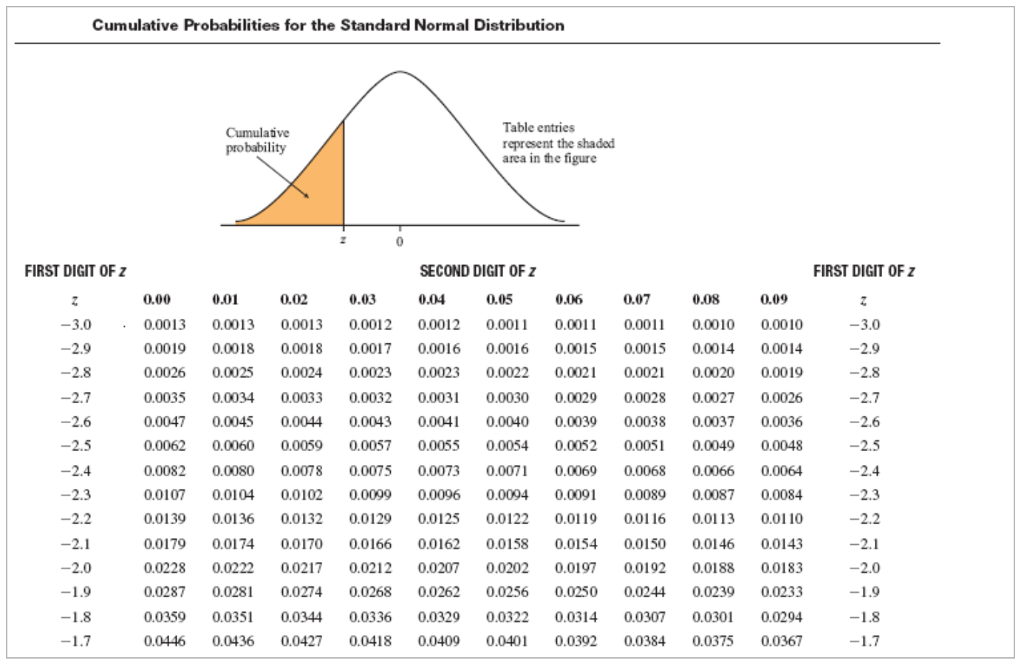
Photo Credit by: bing.com / normal cumulative standard probabilities distribution probability table area solved text digit second problem been