Probability distribution discrete
Table of Contents
Table of Contents
If you’re interested in probability theory and statistics, you’ve likely heard of “Standard Deviation Of A Discrete Probability Distribution.” This concept is fundamental to understanding the properties of any statistical distribution. In this blog post, we’ll dive deep into the topic of Standard Deviation Of A Discrete Probability Distribution, exploring its purpose and application.
Pain Points Related to Standard Deviation Of A Discrete Probability Distribution
Without realizing it, many people struggle with the concept of Standard Deviation Of A Discrete Probability Distribution. Understanding what it is and its purpose is not always an easy task. However, those working in the fields of finance, engineering, or science, where probabilistic models are common, need to master this concept to evaluate and predict the behavior of their systems. By failing to understand Standard Deviation Of A Discrete Probability Distribution’s role, people can make significant errors in their work.
Answering the Target of Standard Deviation Of A Discrete Probability Distribution
Standard Deviation Of A Discrete Probability Distribution measures the amount of variability or dispersion of a probability distribution of a discrete random variable around its expected value. It indicates how much the values vary from the average. A low standard deviation indicates that most values are very close to the mean value, while a high standard deviation demonstrates that the values are spread out over a more extensive range. Standard deviation is one of the key concepts in statistics and probability theory and plays a vital role in many fields, from research to finance to engineering.
Summary of Main Points Related to Standard Deviation Of A Discrete Probability Distribution
Standard deviation of a discrete probability distribution measures how much the values vary from the expected value. A high standard deviation shows that the values are spread out over a larger range, while a low standard deviation indicates that most values are very close to the mean value. Understanding this concept is crucial in many fields, from research to finance to engineering. Whether you are exploring the probability of a random event or working to devise mathematical models of complex systems, you need to understand and work with the concept of Standard Deviation Of A Discrete Probability Distribution.
The Target of Standard Deviation Of A Discrete Probability Distribution
Standard Deviation Of A Discrete Probability Distribution’s primary purpose is to help people understand how close or how far from the mean values are in a discrete probability distribution. This concept provides insight into how the values are dispersed and how likely it is that a value will be reasonably close to or different from the mean value.
In my personal experience, I have used Standard Deviation Of A Discrete Probability Distribution to analyze the reliability of a website. I analyzed the frequency of crashes or malfunctions over time to detect any patterns and assess the site’s overall performance. Using this concept allowed me to pinpoint issues and create models to predict potential future problems.
Applications of Standard Deviation Of A Discrete Probability Distribution
Standard Deviation Of A Discrete Probability Distribution has numerous applications in domains such as engineering, economics, finance, physics, and psychology. In engineering, standard deviation can provide insight into the range of potential outcomes in a specific process or product. In finance, it can indicate the level of risk attached to assets or portfolios. In psychology, it can be used to understand the distribution of responses on any given test.
Specifically, in economics, Standard Deviation Of A Discrete Probability Distribution can show the range of potential stock prices or returns in an investment portfolio. It is also crucial in physics, where it can show the range of energy levels in a quantum system or the level of noise in signal processing. Overall, understanding Standard Deviation Of A Discrete Probability Distribution is critical to making informed decisions and predictions in many fields.
The Calculation of Standard Deviation Of A Discrete Probability Distribution
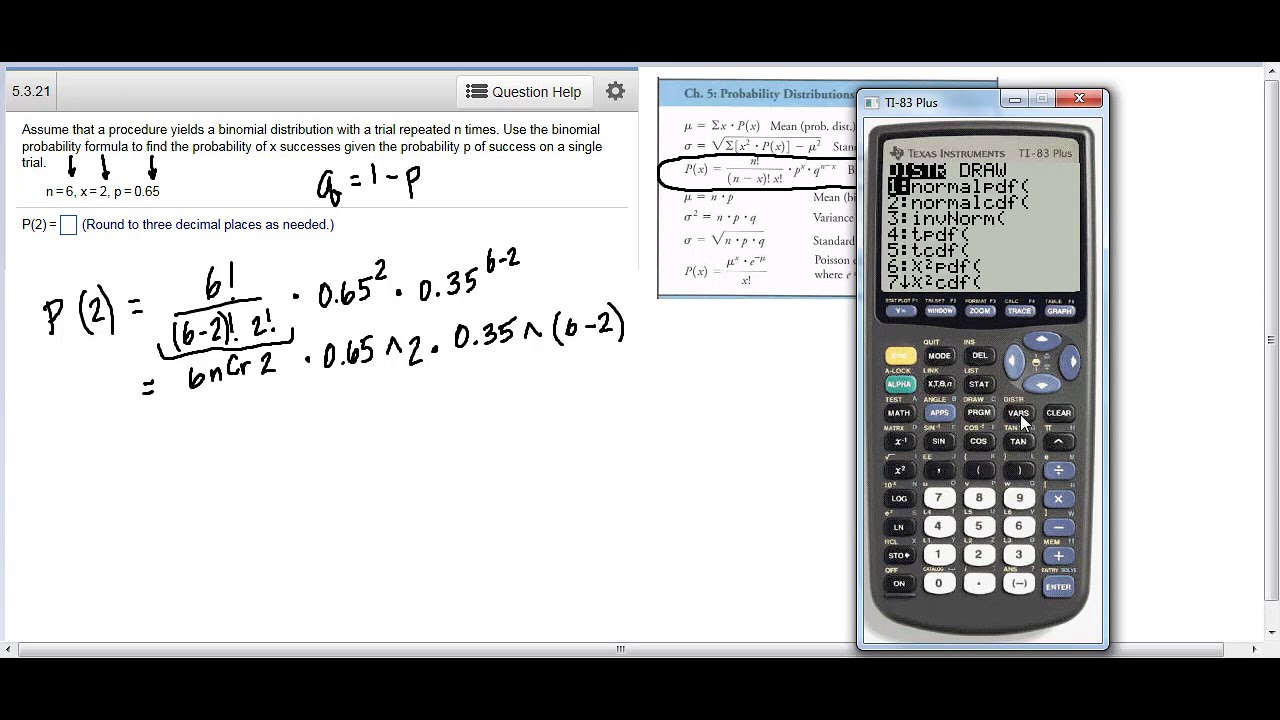
Calculating Standard Deviation Of A Discrete Probability Distribution requires a series of steps. First, determine the expected value based on the probability distribution. Next, find the difference between each value in the probability distribution and the expected value, square that value, and multiply it by its probability. Finally, add the results of each value together and take the square root of that sum.
Understanding the Standard Deviation Of A Discrete Probability Distribution Formula
The formula for Standard Deviation Of A Discrete Probability Distribution is relatively straightforward. It is the square root of the sum of the squared differences between each data point and the mean, divided by the number of data points. Once you calculate the standard deviation, it can be used to understand the range of potential outcomes and assess the risk associated with them.
Real-World Example of Standard Deviation Of A Discrete Probability Distribution
Suppose you are an investor with a $100,000 portfolio and want to evaluate your investment performance between two stocks. One stock has an expected return rate of 15%, and the other has an expected return rate of 20%. In evaluating both choices, standard deviation must be taken into account to understand the risk involved.
The first stock has a standard deviation of 10%, while the second stock has a standard deviation of 25%. The higher standard deviation of the second stock indicates that there is more risk associated with it, as the returns are more spread out around the expected value of 20%.
Question and Answer Section
What is a Discrete Probability Distribution?
A discrete probability distribution is a probability distribution that describes a random variable’s possible outcomes and their associated probabilities. It is used to determine the likelihood of events that can only take on a finite set of values.
What is the Difference Between Discrete and Continuous Distributions?
A discrete distribution deals with random variables that take on a finite set of values, whereas a continuous distribution deals with random variables that can take on an infinite number of possible values.
What is the Purpose of Calculating Standard Deviation?
Standard deviation measures the amount of variability or dispersion of data points in a set of values. It provides insight into how closely values are clustered around the mean and indicates the range of potential outcomes.
What is a High Standard Deviation?
A high standard deviation indicates that the data points are spread out over a larger range relative to the mean value. It suggests that the values are more likely to be further away from the mean value.
Conclusion of Standard Deviation Of A Discrete Probability Distribution
Standard Deviation Of A Discrete Probability Distribution is vital to understanding the distribution of values in many fields, from business to science. It measures the amount of variability or dispersion of data points in a set relative to the mean value and informs predictions and decision-making processes. By understanding this concept, people are better equipped to assess the risk of their investments, predict potential future problems, and evaluate the potential of a set of data points.
Gallery
Discrete Probability Distributions: Finding Probabilities, Expected
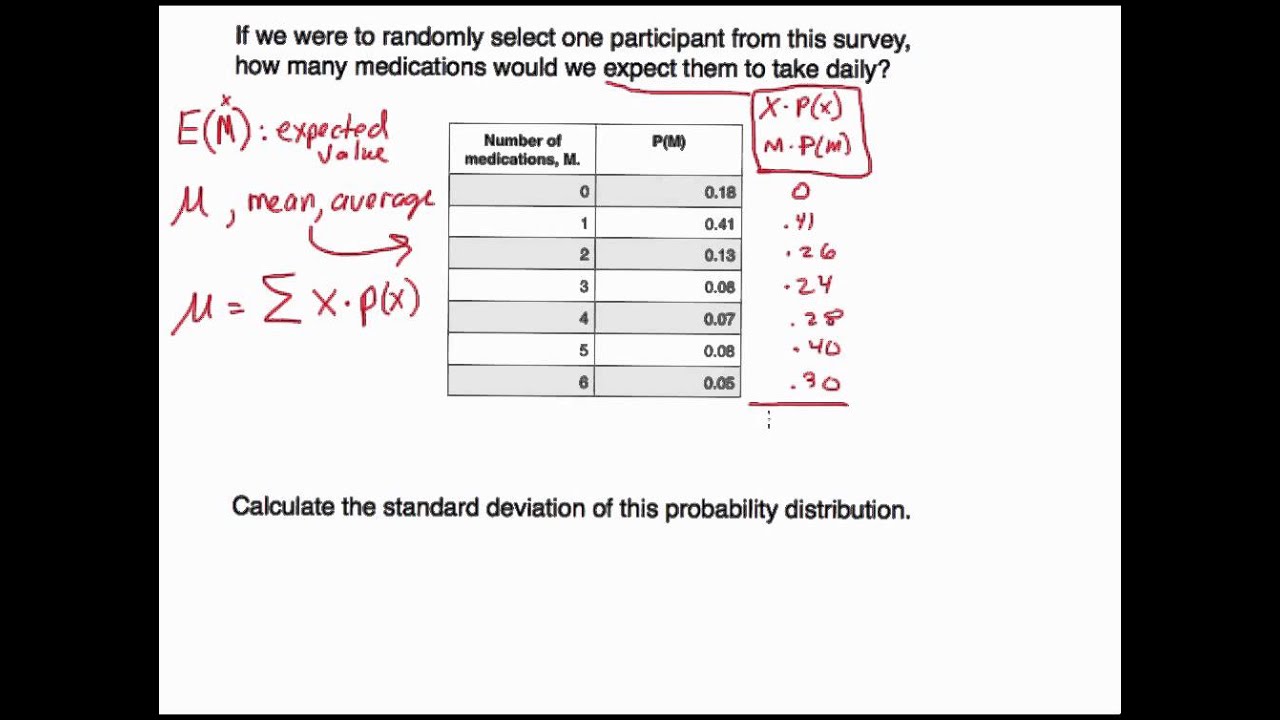
Photo Credit by: bing.com / probability deviation standard discrete expected value finding probabilities distributions
PPT - Chapter 5 Discrete Random Variables And Probability Distributions

Photo Credit by: bing.com / deviation standard discrete random probability variance variables distributions variable chapter example compute ppt powerpoint presentation
PPT - Chapter 6: Discrete Probability Distributions PowerPoint

Photo Credit by: bing.com / probability discrete deviation distribution standard distributions chapter example ppt powerpoint presentation
Standard Deviation Of A Discrete Probability Distribution - YouTube

Photo Credit by: bing.com / probability distribution discrete
Construct A Probability Distribution Calculator - Research Topics

Photo Credit by: bing.com / probability discrete variables construct parameters