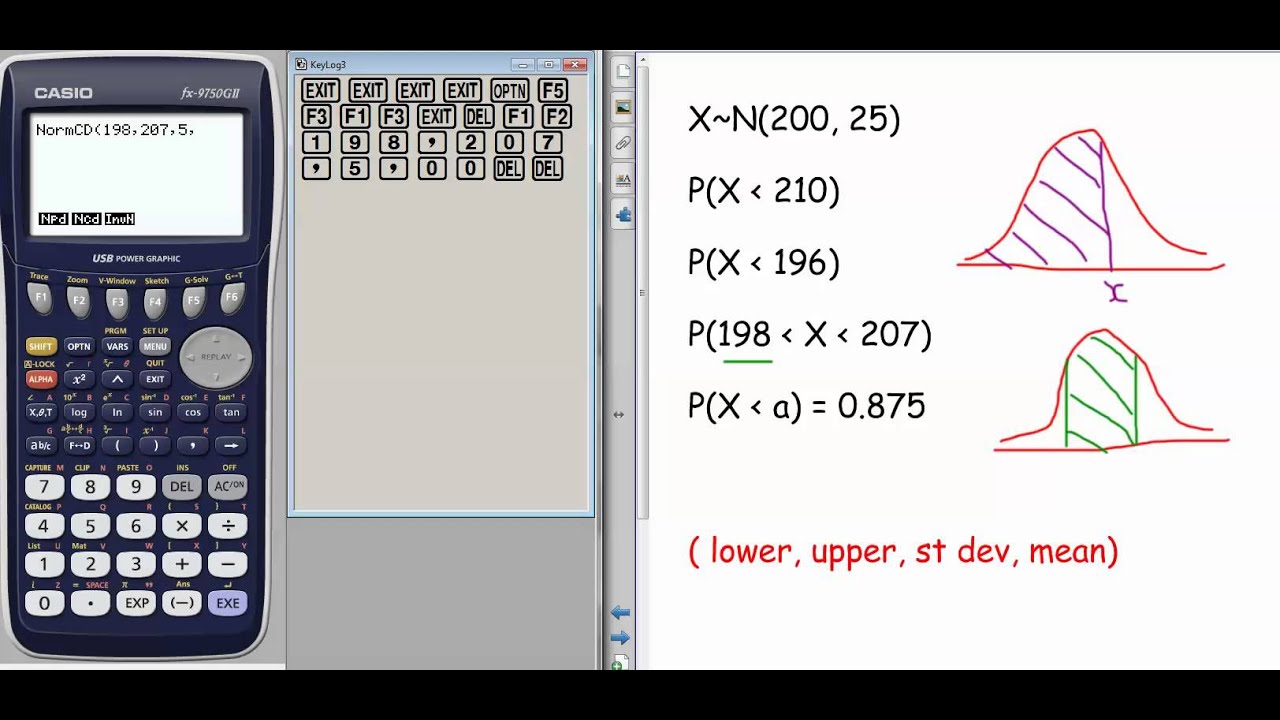
Probability asymptotic properties
Table of Contents
Table of Contents
Have you ever heard of the term “normal distribution”? It is a statistical concept that has been used for over two centuries to describe how data is distributed. In this blog post, we will dive deeper into the properties of the normal probability curve and how it is used in various fields.
Have you ever experienced difficulty analyzing a set of data and determining how it is distributed? This is a common pain point for many individuals working in fields such as finance, statistics, and engineering. Understanding the properties of the normal probability curve can help alleviate some of these difficulties and provide a clearer understanding of the underlying data.
The target of the normal probability curve is to identify the probability distribution of a set of data. This allows individuals to determine the likelihood of certain outcomes occurring, as well as calculating the average and standard deviation of the dataset. By understanding the properties of the normal distribution, individuals can gain a deeper understanding of the data and more accurately draw conclusions from it.
In summary, the normal probability curve is a statistical concept used to describe the distribution of data. By understanding its properties, individuals can gain a deeper understanding of the data and its underlying distribution. The normal distribution is widely used in fields such as finance, statistics, and engineering to make informed decisions based on data analysis.
What are the properties of the normal probability curve?
The normal probability curve has several important properties that distinguish it from other probability distributions. One of the most notable properties is that it is symmetrical around the mean, with the majority of data points clustered around this central value. Additionally, the normal distribution is continuous, meaning that it can take on any value within a certain range.
Another important property of the normal distribution is that it is asymptotic at both ends, meaning that the curve approaches but never touches the horizontal axis. This implies that there is always a probability, no matter how small, of extreme values occurring. The overall shape of the curve is also determined by the mean and standard deviation of the dataset.
How is the normal probability curve used in finance?
One of the most common applications of the normal probability curve in finance is in calculating the returns of investments. By assuming that returns are normally distributed, analysts can calculate the probability of certain outcomes occurring and use this information to make informed investment decisions.
For example, if an investment has a mean return of 8% and a standard deviation of 15%, an analyst can use the normal distribution to determine the probability of the investment returning a certain percentage over a given period of time. This information can then be used to make informed decisions about buying or selling the investment, or adjusting its position within a portfolio.
### What is the relationship between the central limit theorem and the normal distribution?
The central limit theorem states that as the sample size of a dataset increases, the distribution of sample means approaches a normal distribution. This means that even if the underlying data is not normally distributed, the distribution of sample means will become normally distributed as the sample size increases.
This relationship between the central limit theorem and the normal distribution is important in statistics, as it allows analysts to make inferences about the population mean even if the sample size is small or the underlying distribution is unknown.
What are some common misconceptions about the normal probability curve?
One common misconception about the normal probability curve is that it can only be used to describe bell-shaped curves. While the normal distribution is typically bell-shaped, it can take on many different shapes depending on the mean and standard deviation of the dataset.
Another common misconception is that the normal distribution is the only probability distribution used in statistics. While the normal distribution is widely used, there are many other distributions that are specific to certain types of data, such as the Poisson distribution for counting data or the binomial distribution for discrete data.
Conclusion of Properties Of Normal Probability Curve
Understanding the properties of the normal probability curve is essential in many fields, especially finance and statistics. By understanding its properties and applications, analysts can make informed decisions based on data analysis and draw more accurate conclusions from their datasets.
Gallery
Standard Normal Distribution | Quantra By QuantInsti
Photo Credit by: bing.com / normal distribution standard properties
6.1 Graphs Of Normal Probability Distributions X Important Properties
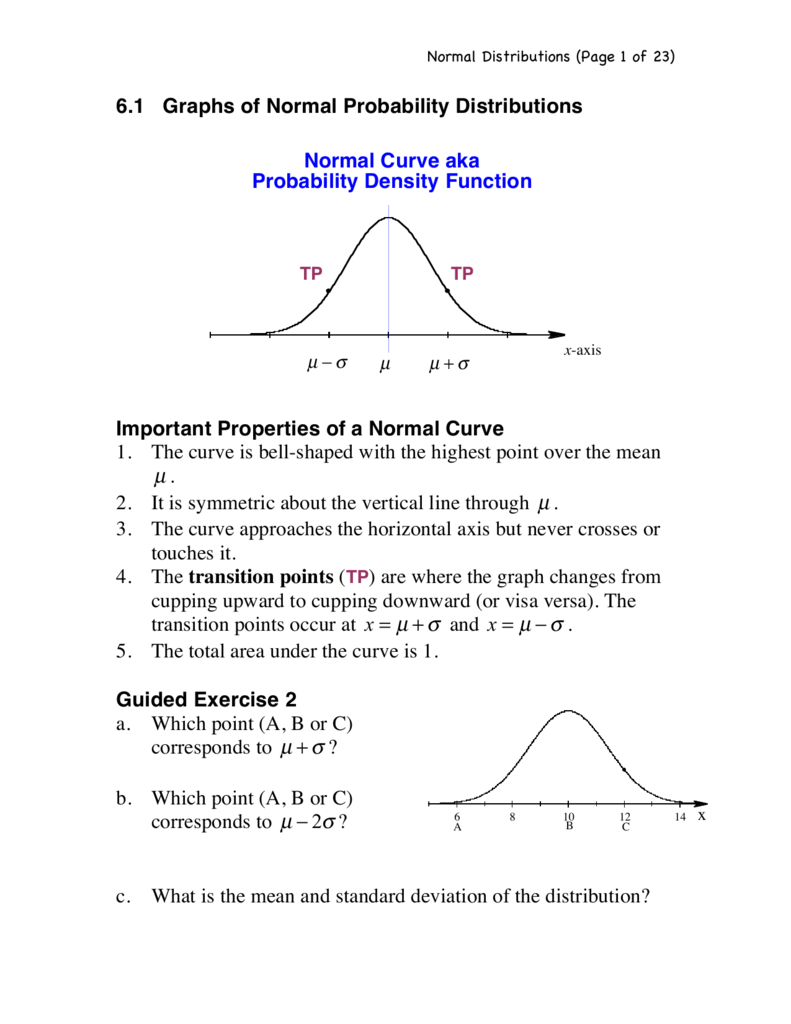
Photo Credit by: bing.com / normal probability distributions properties curve graphs important function
Key Properties Of The Normal Distribution | CFA Level 1 - AnalystPrep
Photo Credit by: bing.com / normal distribution properties shape standard mean variance deviation bell sigma distributions level key cfa useful finance make
The Normal Probability Distribution Is Asymptotic At Both Ends : Slazokas
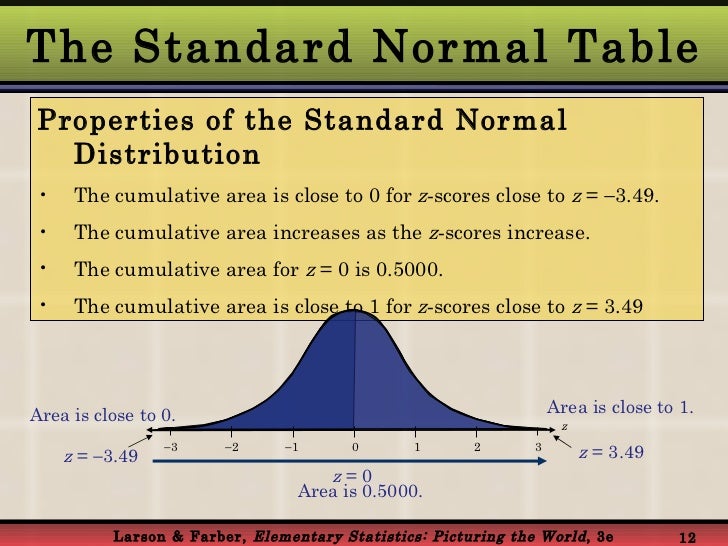
Photo Credit by: bing.com / probability asymptotic properties
PPT - Normal Probability Distributions PowerPoint Presentation, Free
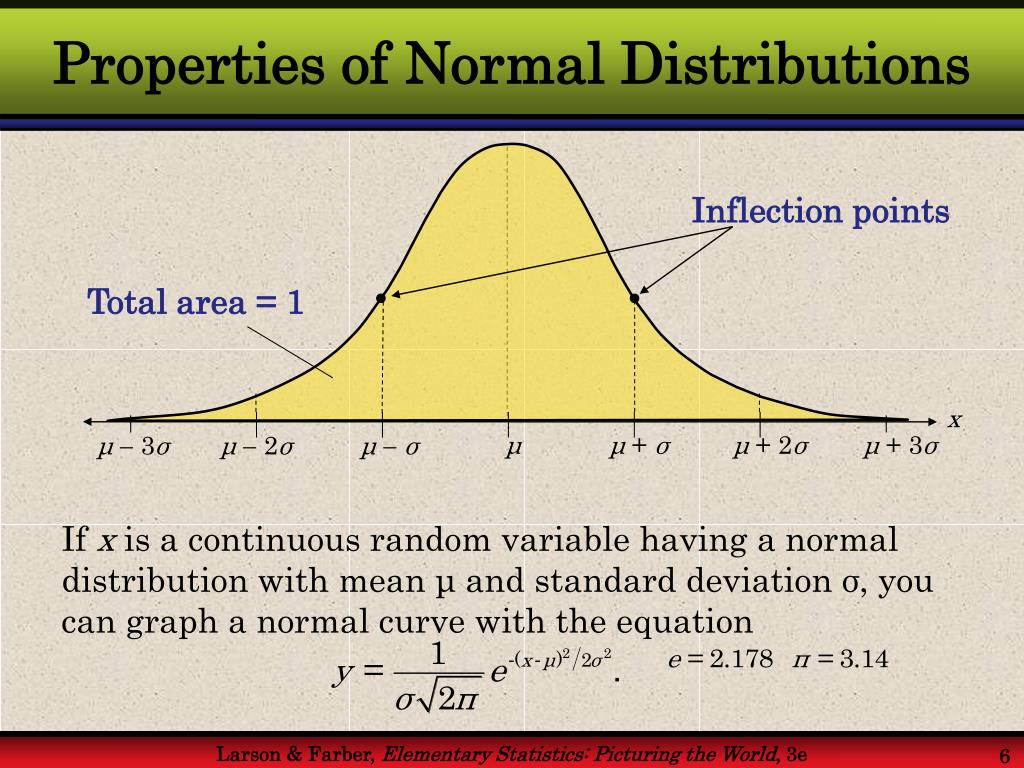
Photo Credit by: bing.com / normal probability distributions ppt powerpoint presentation distribution properties standard mean slideserve
