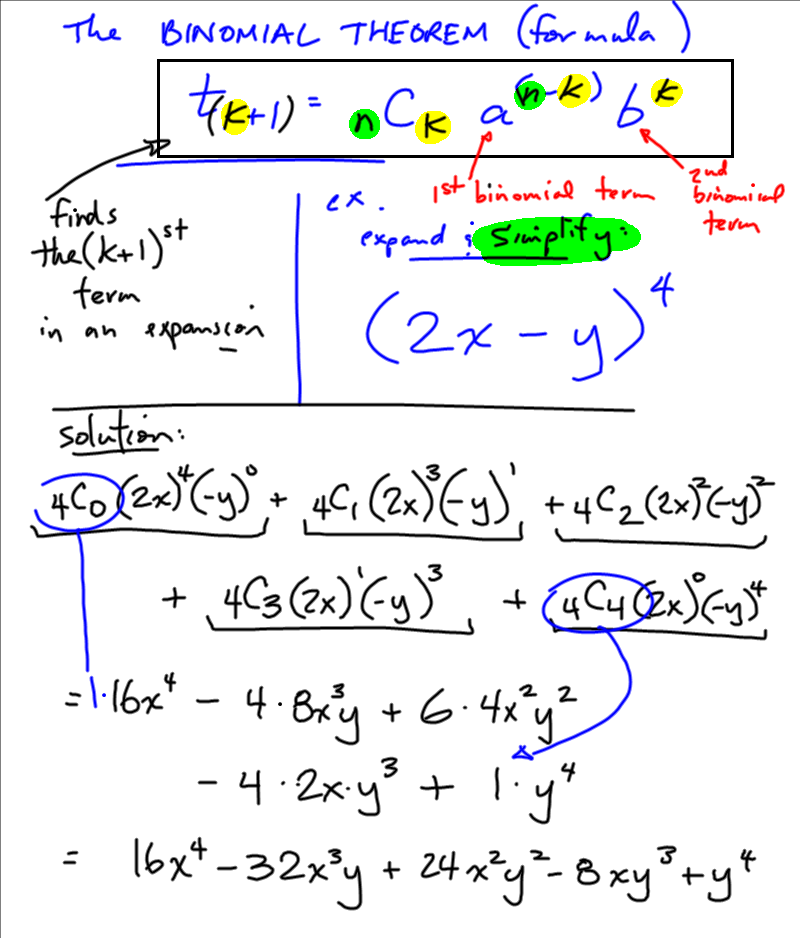
Probability conditional math problems
Table of Contents
Table of Contents
Do you struggle with understanding conditional probability? Are you constantly encountering complex probability problems that make your head spin? If so, you’re not alone. Many students and professionals alike struggle with the concepts and applications of conditional probability, but there are strategies to overcome these challenges.
The Pain Points of Problems on Conditional Probability
Conditional probability is a challenging area of mathematics that requires a solid foundation in probability theory to fully understand. Many people struggle with the concept of dependent and independent events, and how they relate to probability calculations. Additionally, it can be difficult to identify and apply the correct probability formula in a given problem, especially when multiple events are involved.
The Target of Problems on Conditional Probability
The aim of problems on conditional probability is to help students and professionals understand how to calculate the probability of an event occurring given that another event has already occurred. This involves using various probability formulas and rules, such as Bayes’ theorem and the multiplication rule, to calculate conditional probabilities in various real-world applications.
Summary of Main Points
In summary, Problems on Conditional Probability is a complex topic that requires a solid foundation in probability theory. Common pain points include difficulty identifying dependent and independent events, selecting the correct probability formula, and applying the formula in real-world scenarios. Despite these challenges, there are strategies and techniques you can use to master conditional probability and apply it in your academic or professional work.
The Target of Problems on Conditional Probability
Problems on conditional probability can be intimidating at first, but with practice and persistence, you can master this topic. One strategy that has helped me in the past is using concrete examples to illustrate complex concepts. For example, consider a scenario where you have two coins. The first coin is a regular coin, while the second coin is a biased coin with a 70% chance of landing on heads. What is the probability that both coins will land on heads?
By breaking down the problem into smaller components and applying the multiplication rule, we can solve for the probability of both coins landing on heads:
P(both heads) = P(heads on first coin) x P(heads on second coin given heads on first coin)
= 1/2 x 0.7
= 0.35
So, the probability of both coins landing on heads is 0.35 or 35%. Remember, practice is key to understanding and applying conditional probability concepts in real-world problems.
Conditional Probability in Real-World Scenarios
Conditional probability has a wide range of applications in various industries and fields. For example, it can be used in insurance and risk management to calculate the probability of high-risk events or in finance to calculate the probability of stock prices increasing given certain economic conditions. In healthcare, conditional probability can be used to calculate the probability of a patient having a certain disease given a set of symptoms.
Understanding conditional probability is crucial in making informed decisions in high-stakes situations, and can help professionals in various fields make data-driven decisions.
The Nitty Gritty of Conditional Probability
Conditional probability involves calculating the probability of an event occurring given some other related event has already occurred. The formula for conditional probability is:
P(A|B) = P(A and B) / P(B)
where, P(A|B) represents the probability of event A occurring given that event B has already occurred. P(A and B) represents the probability of both events A and B occurring simultaneously, while P(B) represents the probability that event B has occurred.
By using this formula and applying various probability rules, such as Bayes’ theorem or the multiplication rule, you can solve complex conditional probability problems.
The Importance of Conditional Probability
Conditional probability is a fundamental concept in probability theory and has numerous applications in real-world scenarios. By understanding how to calculate conditional probabilities and apply them in various fields, you can make informed decisions and predictions based on data and evidence.
Question and Answer Section
Q1: What is the difference between dependent and independent events?
A1: In probability theory, independent events are events that do not affect each other, while dependent events are events that do affect each other. For example, if you flip a coin and roll a dice, these are independent events since the outcome of one does not affect the outcome of the other. However, if you draw two marbles from a bag without replacement, the second event is dependent on the outcome of the first event.
Q2: What is Bayes’ theorem?
A2: Bayes’ theorem is a probability formula that helps you calculate the probability of an event occurring given some evidence or new information. It involves using prior probabilities and likelihood ratios to update our beliefs about the probability of an event occurring.
Q3: Can conditional probability be used in machine learning?
A3: Yes, conditional probability is a key concept in machine learning, particularly in classification and prediction tasks. By using conditional probabilities, machine learning algorithms can make informed decisions based on new data and evidence.
Q4: What are some real-world applications of conditional probability?
A4: Conditional probability has a wide range of applications in various fields, including insurance and risk management, finance, healthcare, and engineering. It can be used to calculate the probability of high-risk events, predict stock prices, diagnose diseases, and design reliable systems, among other things.
Conclusion of Problems on Conditional Probability
Problems on Conditional Probability can be challenging, but with practice and persistence, you can master this topic. Understanding conditional probability is essential in making informed decisions and predictions based on data and evidence in various fields. Whether you’re a student or a professional, understanding and applying conditional probability can help you succeed in your academic and professional pursuits.
Gallery
41-1 Understanding Conditional Probability - YouTube
Photo Credit by: bing.com / probability conditional
2 3 A Conditional Probability - YouTube
Photo Credit by: bing.com / conditional probability
A Conditional Probability Video - YouTube
Photo Credit by: bing.com / conditional probability
Problems In Conditional Probability | Math | ShowMe
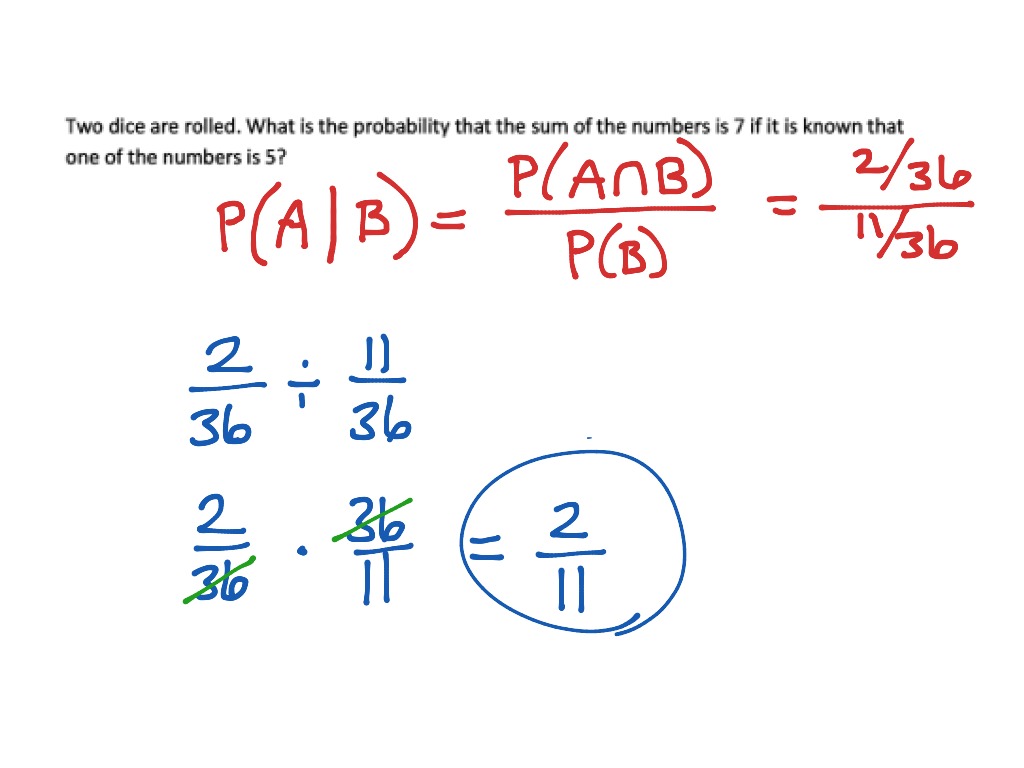
Photo Credit by: bing.com / probability conditional math problems
Conditional Probability - Example 1 | Conditional Probability
Photo Credit by: bing.com / probability conditional contingency
