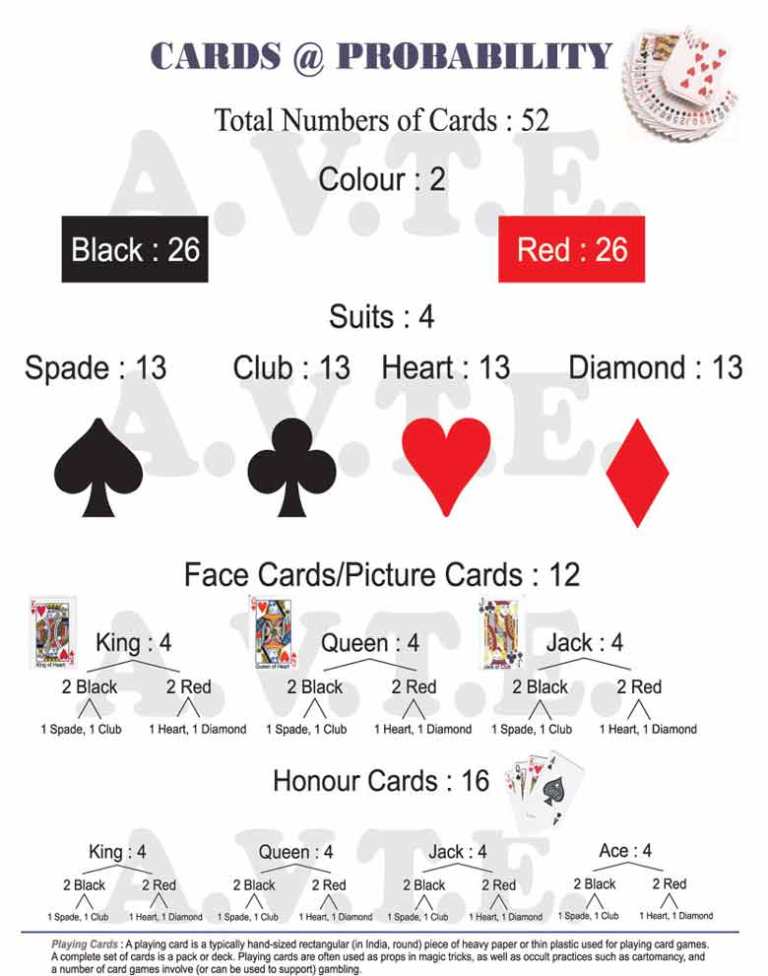
Independent and dependent events conditional probability
Table of Contents
Table of Contents
Are you struggling to understand Probability Of Independent Events? Do you want to know how to calculate the likelihood of two independent events occurring together? If so, you’ve come to the right place. In this article, we will explore everything you need to know about Probability Of Independent Events and how it can help you in your day-to-day life.
Pain Points
Probability Of Independent Events can be a complex topic for many people. It involves understanding the likelihood of multiple events occurring together, which can be difficult to calculate. Additionally, understanding the difference between independent and dependent events can also be confusing. Without a good understanding of these concepts, it can be challenging to make informed decisions.
What is Probability Of Independent Events?
Probability Of Independent Events is the likelihood of two or more events occurring at the same time, where the occurrence of one event does not affect the probability of the other event. For example, flipping a coin twice is an example of two independent events. The outcome of the first coin flip will not affect the outcome of the second coin flip.
Summary
Probability Of Independent Events is a measure of the likelihood of two or more events occurring independently of each other. This can be a complex topic, but it is essential for making informed decisions. Understanding the difference between independent and dependent events is also critical.
Target of Probability Of Independent Events
The target of Probability Of Independent Events is to calculate the likelihood of two or more independent events occurring together. This can be useful in many real-life situations, such as in finance, sports, or gambling. By understanding the probability of independent events, you can make more informed decisions.
For example, let’s say you are a sports bettor, and you want to bet on two different games. You could calculate the probability of each game independently and then calculate the probability of both games happening together. This would help you make a more informed bet.
Examples of Probability Of Independent Events
One personal example of Probability Of Independent Events occurred while I was playing poker with my friends. I had to draw two specific cards from the deck to win the game. I calculated the probability of each card appearing independently and then calculated the probability of both cards appearing together. This helped me make an informed decision on whether it was worth it to continue playing or to fold.
Another example of Probability Of Independent Events occurs in the stock market. Investors often calculate the likelihood of two companies’ stock prices increasing independently and then calculate the probability of both stocks increasing at the same time. This can help them make informed investment decisions.
The Calculation of Probability Of Independent Events
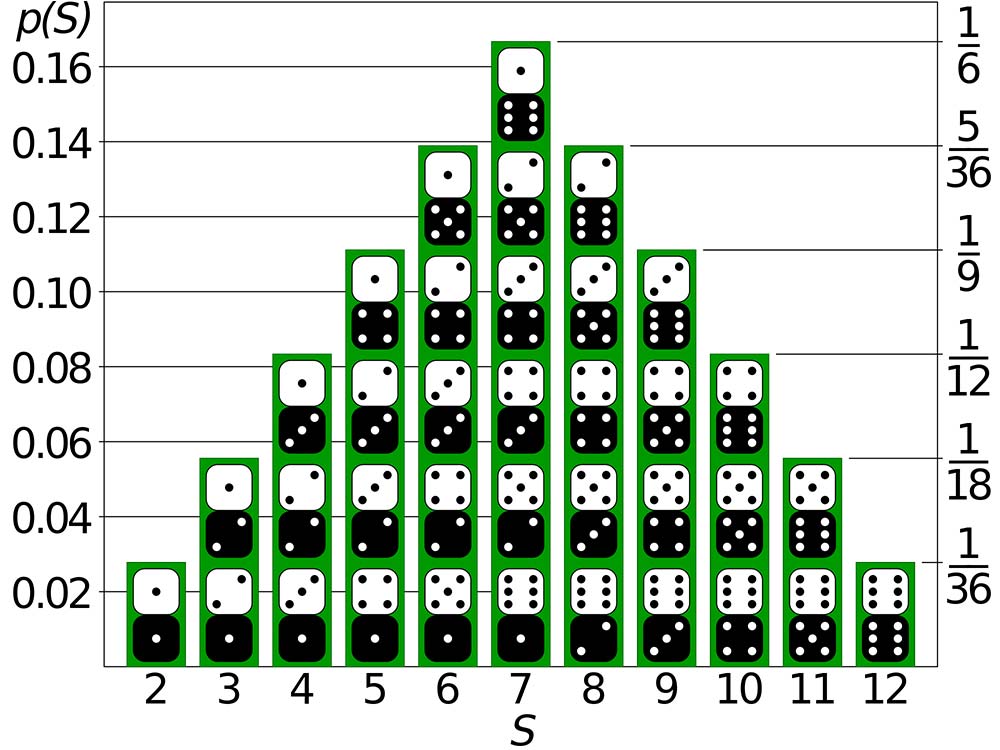
The calculation of Probability Of Independent Events is relatively straightforward. To calculate the probability of two independent events occurring together, you need to multiply the probability of each event occurring independently. For example, the probability of rolling a five on a six-sided dice is 1/6. The probability of rolling another five on a second roll is also 1/6. The probability of rolling two five’s in a row is 1/6 x 1/6 = 1/36.
#### The Importance of Probability Of Independent Events
Probability Of Independent Events is essential for making informed decisions. By understanding the likelihood of two independent events occurring together, you can make better decisions in many real-life situations, such as in finance, sports, or gambling. Additionally, understanding the difference between independent and dependent events is crucial for accurate calculations.
Question and Answer
1. What is the difference between independent and dependent events?
Independent events are events where the occurrence of one event does not affect the probability of the other event. Dependent events are events where the occurrence of one event affects the probability of the other event.
2. Can you give an example of Probability Of Independent Events in real-life?
One example of Probability Of Independent Events in real-life is rolling two dice and calculating the probability of getting a 2 on one dice and a 3 on the other dice.
3. How do you calculate the Probability Of Independent Events?
To calculate the Probability Of Independent Events, you need to multiply the probability of each event occurring independently. For example, the probability of flipping a coin and getting heads is 1/2. The probability of flipping another heads on a second flip is also 1/2. The probability of flipping two heads in a row is 1/2 x 1/2 = 1/4.
4. Why is understanding Probability Of Independent Events important?
Understanding Probability Of Independent Events is crucial for making informed decisions in many real-life situations, such as in finance, sports, or gambling. Additionally, understanding the difference between independent and dependent events is crucial for accurate calculations.
Conclusion of Probability Of Independent Events
In conclusion, Probability Of Independent Events is a critical concept to understand for making informed decisions. By understanding the likelihood of two independent events occurring together, you can make better decisions in many real-life situations. Additionally, understanding the difference between independent and dependent events is crucial for accurate calculations. Hopefully, this article has helped you understand Probability Of Independent Events better and how it can help you in your day-to-day life.
Gallery
Independent Events (Probability)
Photo Credit by: bing.com / independent probability andymath statistics
Independent And Dependent Events; Conditional Probability
Photo Credit by: bing.com / probability conditional dependent cafeteria
Probability-Independent And Dependent Events - YouTube
Photo Credit by: bing.com / independent probability dependent events
PPT - 12.5 Probability Of Independent & Dependent Events PowerPoint
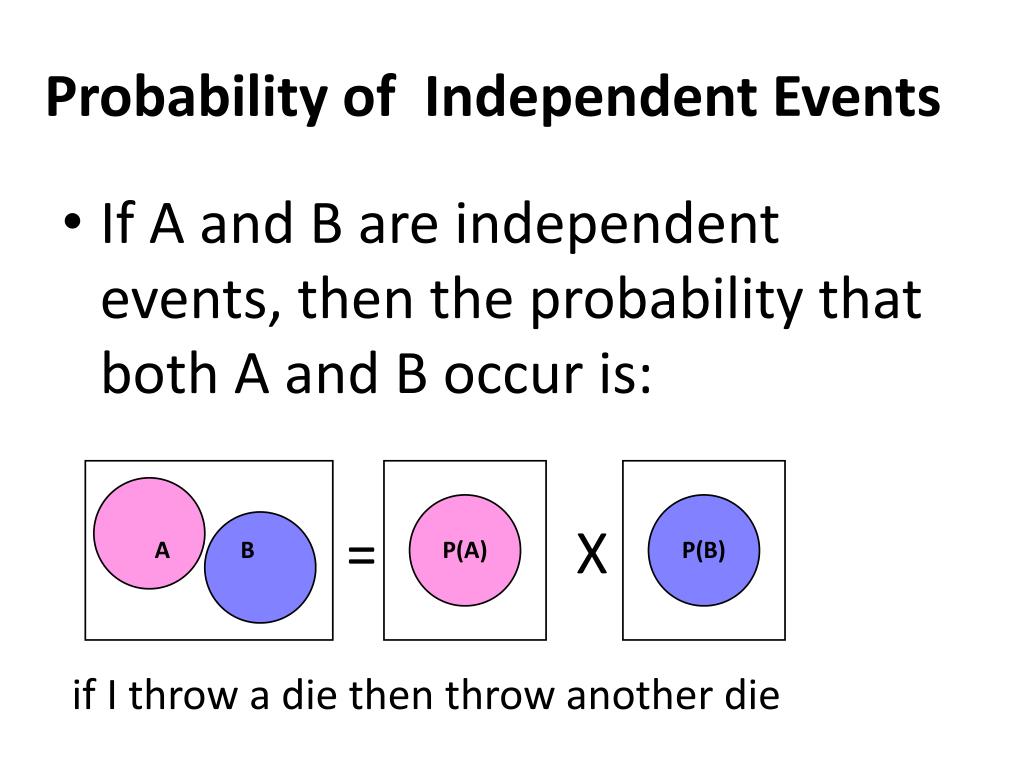
Photo Credit by: bing.com / probability independent events dependent presentation
The Conjunction Problem Is Not A Problem For Bayesians | Prior Probability
Photo Credit by: bing.com / dependent events probability examples independent solutions conjunction event if problem formulas following outcome
