Binomial probability distribution
Table of Contents
Table of Contents
Have you ever heard of the Probability of Binomial Distribution? If not, you’re in for a treat! This powerful concept is a crucial aspect of probability theory, and understanding it can unlock a world of possibilities for data analysis and decision-making.
Pain Points
Probability of Binomial Distribution can be a challenging topic for many individuals. One common pain point is understanding the underlying logic and formulas. Another is knowing how to apply the concept to real-world scenarios. Yet another is interpreting the results and making data-driven decisions based on that information.
What is Probability of Binomial Distribution?
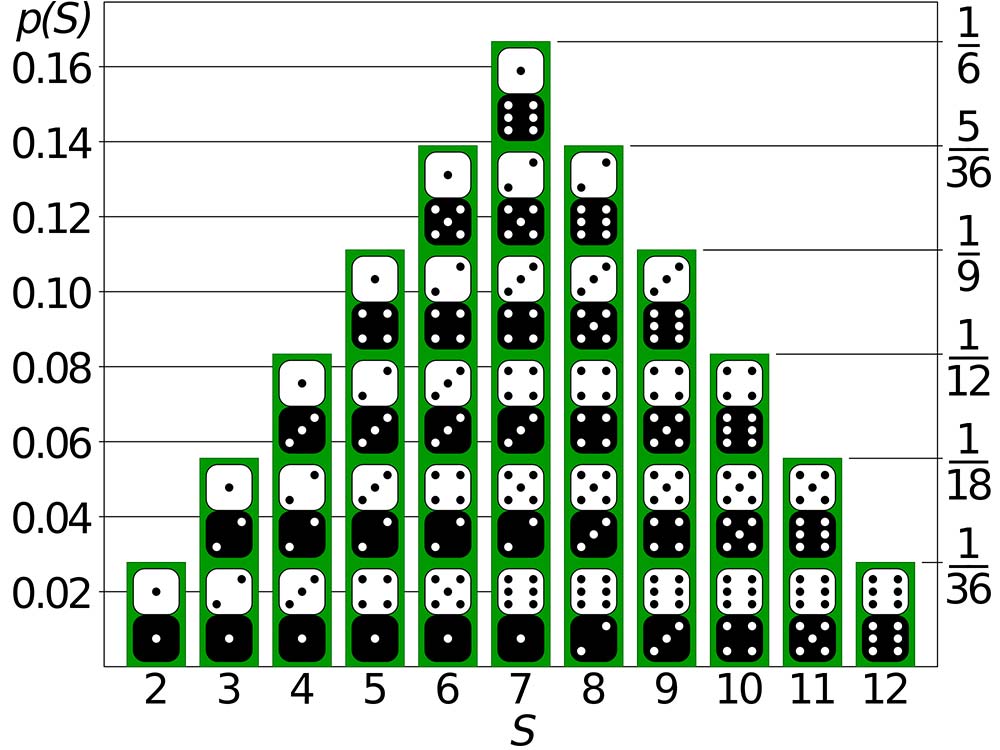
In probability theory, the binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials. For example, if you are conducting a survey and you want to know how many respondents will answer “yes” to a particular question, you can use the binomial distribution to model that outcome.
Main Points
Probability of Binomial Distribution is used to describe the number of successes in a fixed number of independent trials. It is especially useful when dealing with discrete events that have binary outcomes (ie: yes or no). Probability of Binomial Distribution can be challenging to understand, but it is an essential concept for anyone working with data analysis or decision-making.
Target and Personal Experience
The target of Probability of Binomial Distribution is to provide a framework for modeling and predicting the likelihood of binary outcomes. As a data scientist, I have used this concept countless times to analyze survey data, customer satisfaction metrics, and quality control data. By understanding the underlying logic and formulas of Probability of Binomial Distribution, I can make data-driven decisions and recommendations that have a significant impact on the organizations I work with.
Applications of Probability of Binomial Distribution
Probability of Binomial Distribution has many applications across a variety of industries. It is commonly used in quality control, market research, polling, and risk management. For example, a company might use Probability of Binomial Distribution to model the likelihood of product defects in their manufacturing process. Or a political campaign might use Probability of Binomial Distribution to predict the outcome of an election based on polling data.
How to Calculate Probability of Binomial Distribution
The formula for Probability of Binomial Distribution is relatively simple:
P(x) = (n choose x) * p^x * (1-p)^(n-x)
Where n is the number of trials, p is the probability of success, x is the number of successes, and (n choose x) is the binomial coefficient.
Using Probability of Binomial Distribution in Python
Python has several libraries that make it easy to calculate probability of Binomial Distribution. One popular library is scipy.stats, which provides several functions for working with Probability of Binomial Distribution. For example, you can use the binom.pmf function to calculate the probability mass function, or the binom.cdf function to calculate the cumulative distribution function.
Real-World Example of Probability of Binomial Distribution
Let’s say you are conducting a survey of 100 people, and you want to know how many of them prefer Diet Coke over Pepsi. You can use Probability of Binomial Distribution to model this scenario. Let’s assume that 40% of the general population prefers Diet Coke over Pepsi. If we assume that our sample is representative of the general population, we can use the binomial distribution to calculate the likelihood of different outcomes.
P(X=0) = (100 choose 0) * .4^0 * .6^100 = 0.00006
P(X=1) = (100 choose 1) * .4^1 * .6^99 = 0.001288
P(X=2) = (100 choose 2) * .4^2 * .6^98 = 0.011606
Based on these calculations, we can conclude that it is unlikely that none of the respondents prefer Diet Coke over Pepsi. However, it is relatively likely that at least one respondent prefers Diet Coke over Pepsi.
Question and Answer
Q: When should I use Probability of Binomial Distribution?
A: Probability of Binomial Distribution is useful when you are dealing with discrete events that have binary outcomes. This could include surveys, quality control data, polling data, and market research.
Q: Is Probability of Binomial Distribution easy to understand?
A: Probability of Binomial Distribution can be challenging to understand at first, but with practice and experience, it becomes more intuitive. There are also many resources available online that can help you learn the basics of Probability of Binomial Distribution.
Q: What are some common applications of Probability of Binomial Distribution?
A: Probability of Binomial Distribution is commonly used in quality control, market research, polling, and risk management. For example, a company might use Probability of Binomial Distribution to model the likelihood of product defects in their manufacturing process. Or a political campaign might use Probability of Binomial Distribution to predict the outcome of an election based on polling data.
Q: Can I use Python to calculate Probability of Binomial Distribution?
A: Yes, there are several libraries in Python that make it easy to calculate Probability of Binomial Distribution. One popular library is scipy.stats, which provides several functions for working with Probability of Binomial Distribution.
Conclusion of Probability of Binomial Distribution
Probability of Binomial Distribution is a powerful concept that has many applications in data analysis and decision-making. While it may be intimidating at first, understanding the underlying logic and formulas can unlock a world of possibilities. Whether you are dealing with quality control data, market research, or polling data, Probability of Binomial Distribution is a valuable tool for modeling and predicting binary outcomes.
Gallery
PPT - Examples Of Discrete Probability Distributions: PowerPoint

Photo Credit by: bing.com / binomial distribution probability examples distributions discrete example ppt getting powerpoint presentation fewer toss coin heads times if slideserve
Binomial Probability Distribution - Data Science Kernel
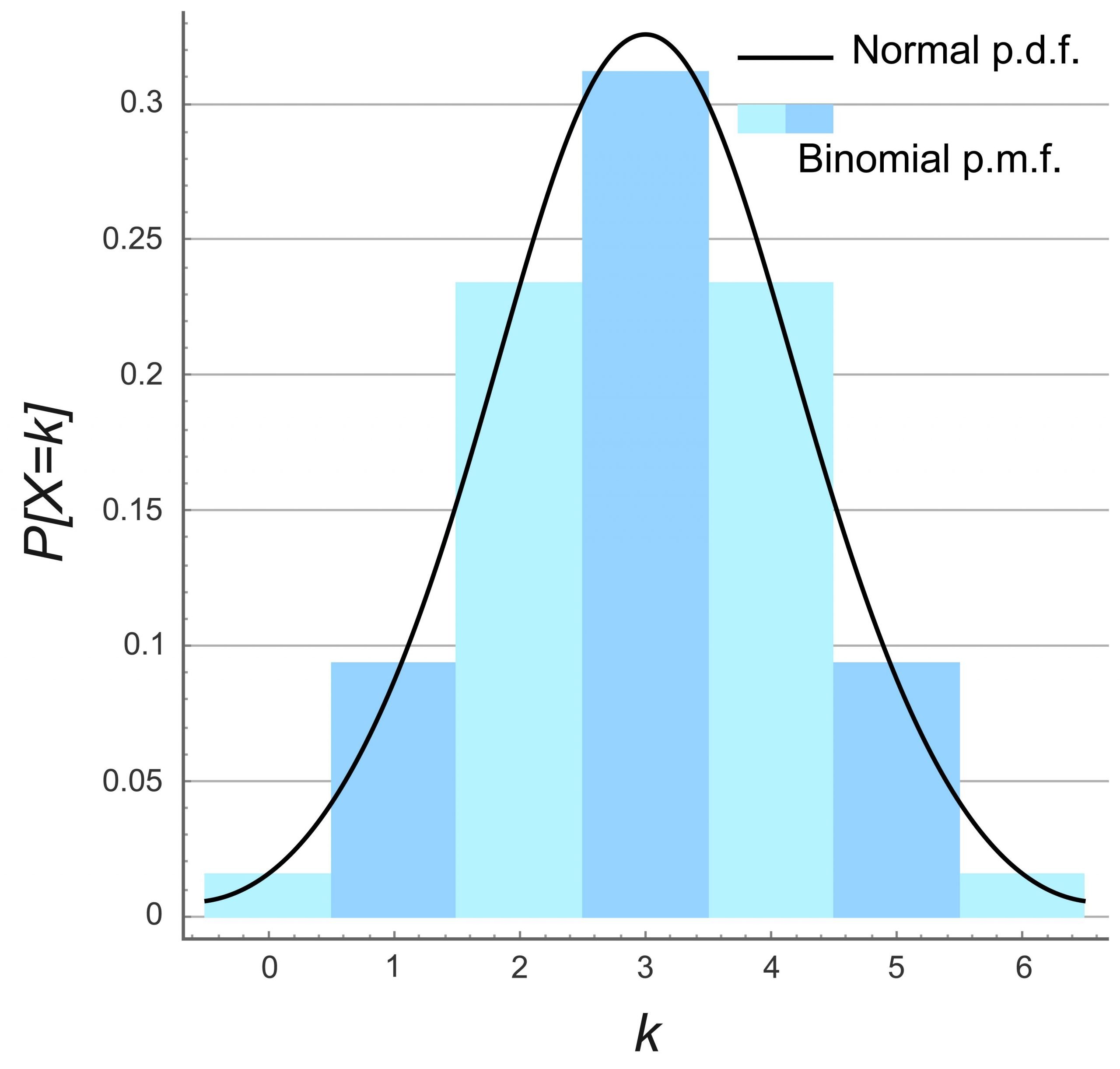
Photo Credit by: bing.com / distribution binomial probability statistics
PPT - Binomial Probability Distribution 1. The Experiment Must Have A

Photo Credit by: bing.com / binomial probability distribution formula experiment trials fixed number method must ppt powerpoint presentation qn px slideserve
PPT - Binomial Probability Distribution PowerPoint Presentation, Free

Photo Credit by: bing.com / binomial distribution probability mean variance ppt success standard deviation cdf trials powerpoint presentation
The Variance For The Binomial Probability Distribution Is - Research Topics

Photo Credit by: bing.com / binomial probability variance