Distribution binomial probability statistics
Table of Contents
Table of Contents
Do you want to understand the probability of a binomial distribution? If you often encounter situations with only two possible outcomes, then this is the probability distribution to understand.
In many scenarios, we are unsure of the outcome of an event, and based on available data, we make predictions. In such cases, understanding the probability of a binomial distribution can be beneficial. Pain points related to probability of a binomial distribution can arise when you need a precise probability estimate with a small sample size. This distribution can also be difficult to calculate if there are multiple outcomes, as opposed to just two.
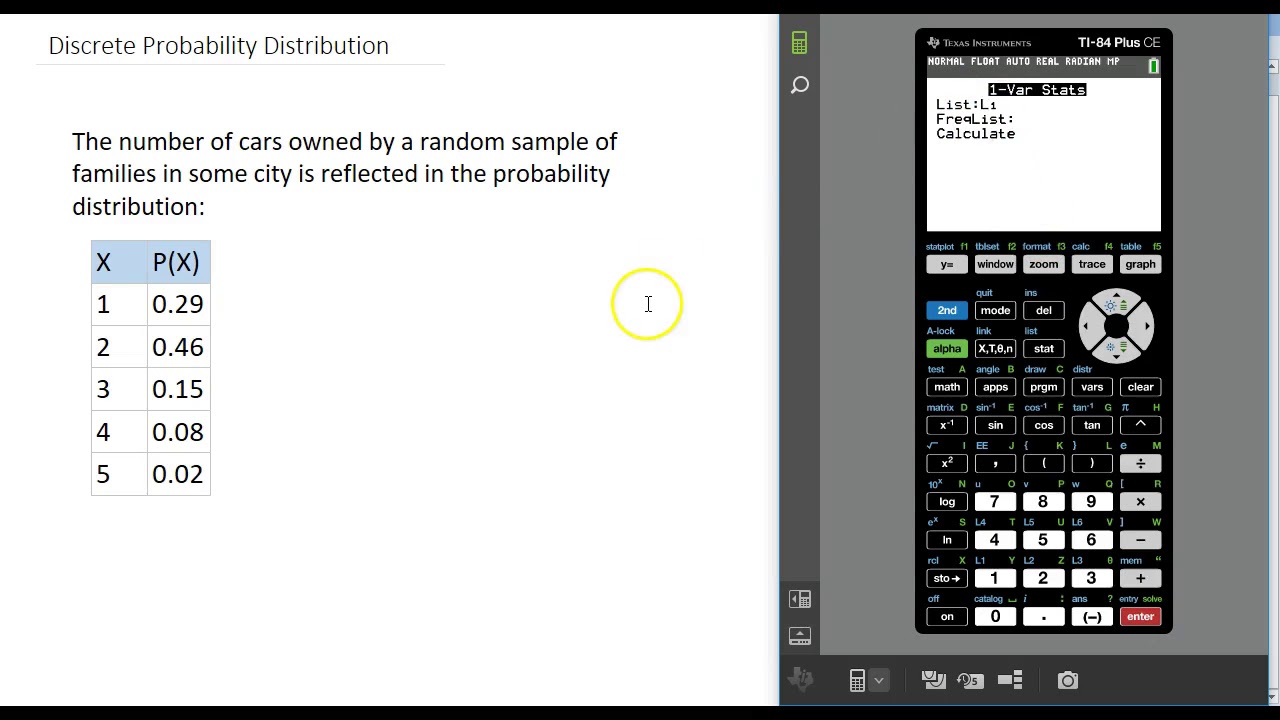
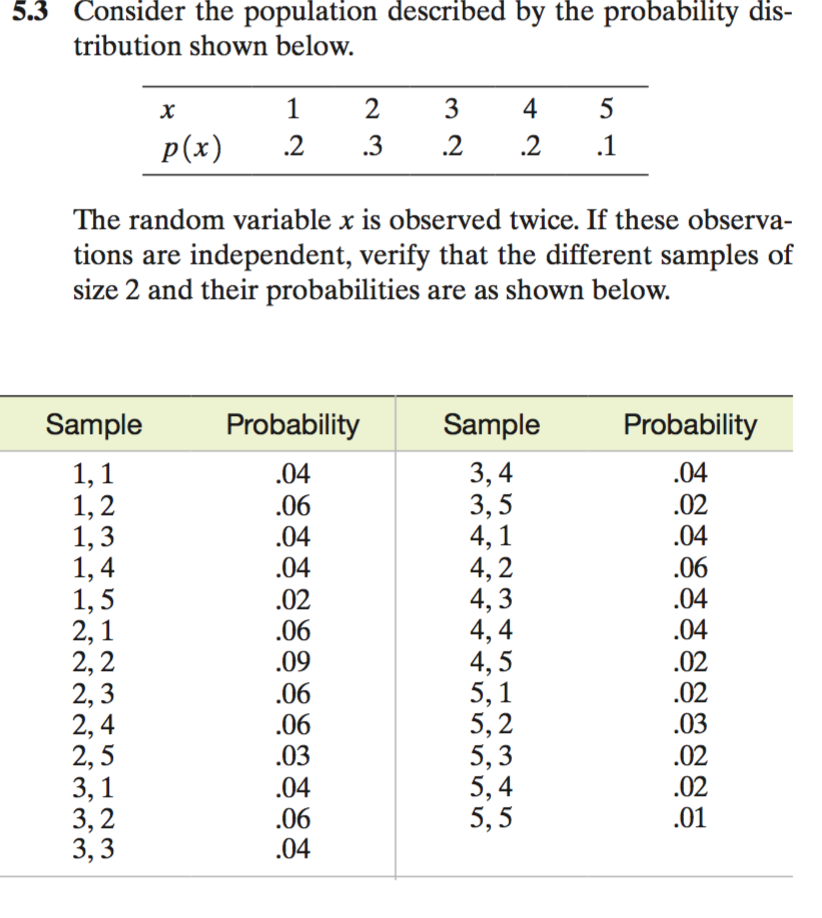
The target of the probability of a binomial distribution is to determine the likelihood of a certain number of successes over a given number of trials, with only two possible outcomes.
To summarize, the probability of a binomial distribution applies to situations with two possible outcomes. Understanding this distribution can be beneficial in making predictions. However, pain points can arise with calculating precise probabilities with a small sample size or multiple outcomes.
Probability Of A Binomial Distribution and its Target
When I first learned about the probability of a binomial distribution, I was running a small business and trying to predict the likelihood of customers converting from leads to sales. Understanding this distribution allowed me to make data-driven decisions and adjust my marketing strategy accordingly. Probability of a binomial distribution determines the likelihood of a specific number of successes over a given number of trials with only two possible outcomes. For example, flipping a coin has only two possible outcomes, heads or tails. This distribution can help calculate the probability of a specific number of heads or tails occurring over a given number of flips.
Use Cases of Probability Of A Binomial Distribution
Another use case for the probability of a binomial distribution could be in the field of medicine. Suppose a new drug is tested on 100 participants. The drug’s success rate can be calculated using this distribution by determining the probability of a certain number of successes (successful recoveries) over 100 trials (participants using the drug).
Calculating Probability Of A Binomial Distribution
The probability of a binomial distribution can be calculated using the following formula:
 The variables used in this formula are:
The variables used in this formula are:
- P(X) is the probability of X successes
- n is the total number of trials
- p is the probability of success
- q is the probability of failure (1-p)
Real-Life Example of Probability Of A Binomial Distribution
Suppose you run an e-commerce business, and you launch a new ad campaign. You can use the probability of a binomial distribution to determine the likelihood of a specific number of clicks over a given number of impressions.
Question and Answer
Q: What is the difference between a binomial distribution and a Poisson distribution?
A: Binomial distributions deal with a fixed number of trials with only two possible outcomes. Poisson distributions deal with incidents that occur randomly and frequently.
Q: Can we use the probability of a binomial distribution for multiple outcomes?
A: No, probability of a binomial distribution is only for two possible outcomes. If there are multiple outcomes, we can use a multinomial distribution.
Q: In which fields can probability of a binomial distribution be used?
A: Probability of a binomial distribution can be used in fields such as finance, marketing, and medicine, where two possible outcomes play a large part in the decision-making process.
Q: What does the sum of the probabilities in a binomial distribution equal to?
A: The sum of probabilities in a binomial distribution is equal to 1.
Conclusion of Probability Of A Binomial Distribution
Probability of a binomial distribution calculates the likelihood of a specific number of successes over a given number of trials with only two possible outcomes. It can be beneficial in various scenarios, including business, medicine, and finance. Understanding this distribution can help make data-driven decisions and calculate probabilities to avoid blind guesses.
Gallery
The Variance For The Binomial Probability Distribution Is - Research Topics

Photo Credit by: bing.com / binomial probability variance
What Is A Probability Distribution - Research Topics

Photo Credit by: bing.com / probability binomial
PPT - Binomial Probability Distribution 1. The Experiment Must Have A

Photo Credit by: bing.com / binomial probability distribution formula experiment trials fixed number method must ppt powerpoint presentation qn px slideserve
Binomial Probability Distribution - Data Science Kernel
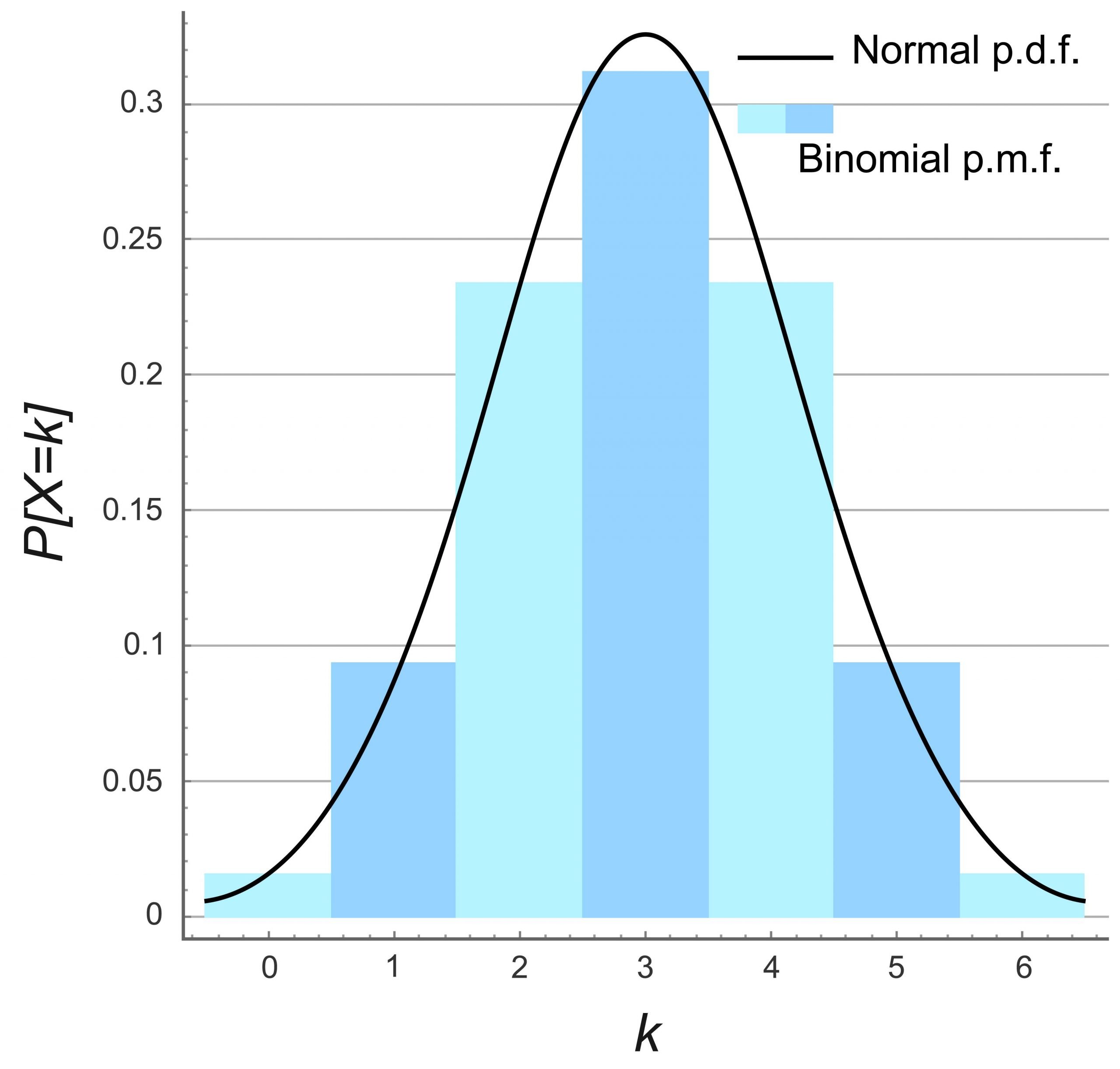
Photo Credit by: bing.com / distribution binomial probability statistics
Binomial Probability Distribution Tutorial

Photo Credit by: bing.com / binomial probability formulas calculate successes onlinemathlearning trials tosses fraction bernoulli roll