Normal Probability Curve Definition

Probability iq statistics normality mind sigma

Table of Contents

The Normal Probability Curve, also known as the Gaussian distribution or bell curve, is a statistical concept that is used throughout many industries and fields of study. From predicting the weather, to analyzing stock markets, to evaluating student test scores, the Normal Probability Curve is a central tool that helps us understand the likelihood of certain events occurring. In this article, we will explore the definition of the Normal Probability Curve in more detail and explain why it is important to understand in today’s data-driven world.

When it comes to data analysis, one of the biggest challenges is dealing with variability. Data can be noisy, messy, and unpredictable, which makes drawing conclusions and making reliable predictions difficult. This is where the Normal Probability Curve comes in. By assuming that data follows a normal distribution, we can use mathematical equations to make predictions about our data with a high degree of confidence. However, understanding the Normal Probability Curve can be challenging for those without a background in statistics, which is why we will break down the concept in more detail below.

The target of the Normal Probability Curve is to provide a mathematical model of a random variable that has a normal distribution. In statistics, a normal distribution is a continuous probability distribution that is symmetric, bell-shaped, and defined by two parameters: the mean and the standard deviation. By assuming a normal distribution, we can make predictions about our data with a high degree of confidence, which is why the Normal Probability Curve is such a valuable tool in the world of data analysis. Essentially, the Normal Probability Curve allows us to quantify the likelihood of certain outcomes and understand how much variability we can expect in our data.

In summary, the Normal Probability Curve is a statistical concept that is used to model normal distributions and make predictions about data with a high degree of confidence. By understanding the Normal Probability Curve, we can better analyze data and make more informed decisions based on that data. Some common use cases for the Normal Probability Curve include predicting the likelihood of weather events, analyzing stock market trends, and evaluating student test scores.

What is the Normal Probability Curve and Why is it Important?

As someone who works with data on a daily basis, I can attest to the importance of the Normal Probability Curve in modern-day analytics. When it comes to predicting outcomes and understanding the variability of data, the Normal Probability Curve is a crucial tool that allows us to make informed decisions. For example, in my work as a data analyst for a retail company, we use the Normal Probability Curve to predict sales patterns and identify outliers that may require further investigation. By leveraging the power of the Normal Probability Curve, we are able to make more accurate predictions and optimize our business processes for better results.

How to Use the Normal Probability Curve in Data Analysis

To use the Normal Probability Curve in data analysis, you first need to understand the concept of a normal distribution. A normal distribution is a probability distribution that is symmetric and bell-shaped, with the majority of data falling within one standard deviation of the mean. By assuming that a dataset follows a normal distribution, you can calculate the probability of certain events occurring and make predictions with a high degree of confidence. For example, if you are trying to predict the likelihood of a stock market crash, you can use the Normal Probability Curve to calculate the probability of such an event occurring based on historical data.

The Benefits of Understanding the Normal Probability Curve

There are many benefits to understanding the Normal Probability Curve, especially in today’s data-driven world. By leveraging statistical concepts like the Normal Probability Curve, we can make more informed decisions and optimize our processes for better results. For example, in healthcare, understanding the Normal Probability Curve can help doctors identify outliers and better predict patient outcomes. Similarly, in finance, the Normal Probability Curve is a crucial tool for predicting stock market trends and identifying risks. In short, the Normal Probability Curve is a key concept that helps us make sense of the world around us and make more informed decisions based on data.

How to Learn More About the Normal Probability Curve

If you are interested in learning more about the Normal Probability Curve and how it can be applied to real-world problems, there are many resources available online. From online courses to tutorials to interactive tools, there are many ways to deepen your understanding of this important statistical concept. Some good places to start include open online courses from universities like MIT and Harvard, as well as popular data science blogs like KDnuggets and Towards Data Science.

Question and Answer

• Q: What is the difference between a normal distribution and a Gaussian distribution?
• A: There is no difference between a normal distribution and a Gaussian distribution. The terms are interchangeable and refer to the same probability distribution.
• Q: What is the central limit theorem?
• A: The central limit theorem is a statistical concept that states that as sample size increases, the distribution of sample means approaches a normal distribution.
• Q: What is the area under the Normal Probability Curve?
• A: The area under the Normal Probability Curve represents the total probability of all possible outcomes. The area under the curve between two points represents the probability of an outcome falling between those two values.
• Q: How is the Normal Probability Curve used in hypothesis testing?
• A: In hypothesis testing, the Normal Probability Curve is used to calculate p-values, which represent the probability of observing a test statistic as extreme as the one observed, assuming the null hypothesis is true.

Conclusion of Normal Probability Curve Definition

The Normal Probability Curve is a statistical concept that is used to model normal distributions and make predictions about data with a high degree of confidence. By leveraging the power of the Normal Probability Curve, we are able to make more accurate predictions and optimize our business processes for better results. Whether you are a data analyst, a healthcare professional, or a finance expert, understanding the Normal Probability Curve is a crucial tool that can help you make better decisions based on data.

Gallery

Image - Normal Curve Probability.jpg | What I Learned Wiki | FANDOM

_{^{Photo Credit by: bing.com / probability iq statistics normality mind sigma}}

The Scores On Standardized Admissions Test Are Normally Distributed

_{^{Photo Credit by: bing.com / distribution normal curve mean bell standard deviation statistics normally distributed explained probability make between scores relationship look simply standardized shifted}}

The Normal Distribution Table Definition

_{^{Photo Credit by: bing.com / normal probability investopedia jiang}}

9 Real Life Examples Of Normal Distribution – StudiousGuy

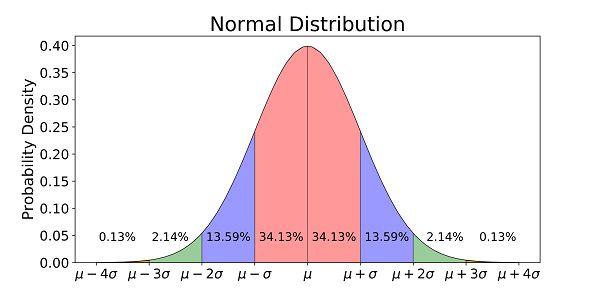
_{^{Photo Credit by: bing.com / normal distribution curve life examples real standard deviation mean graph under width height determines center}}

The Standard Normal Distribution | Examples, Explanations, Uses

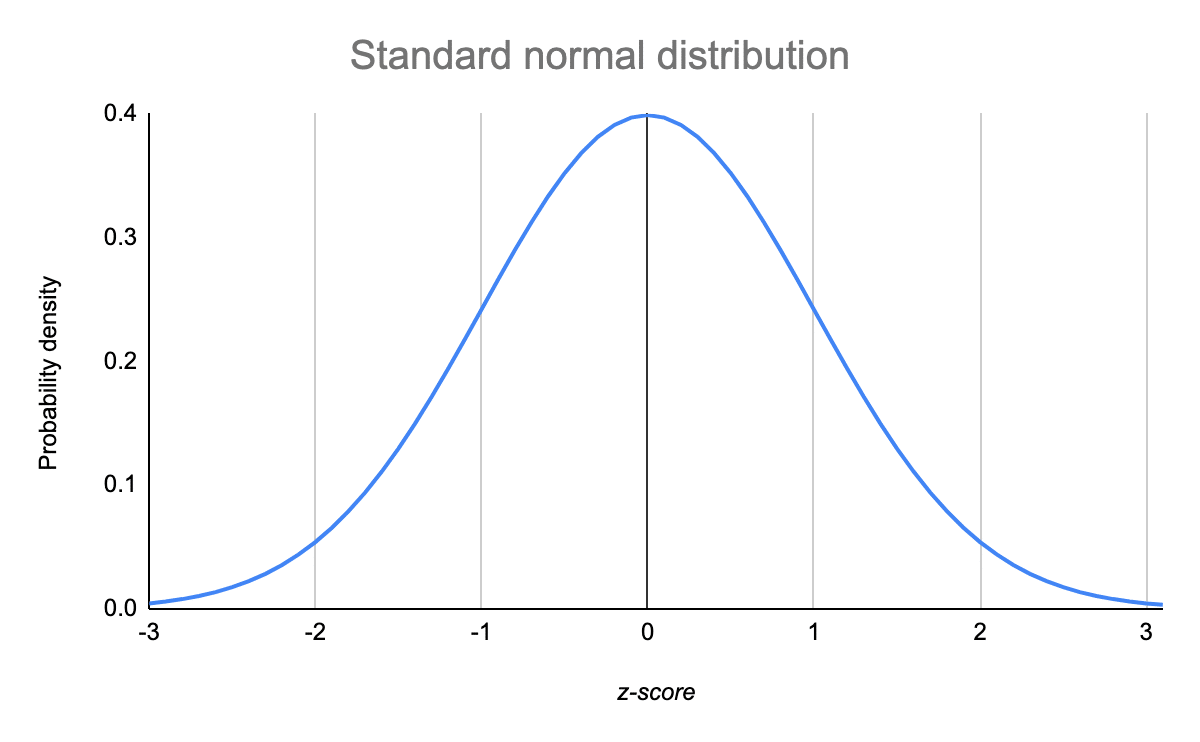
_{^{Photo Credit by: bing.com / probability distributions deviations values statistics standardized latency percentile courses fps bimodal spending converting}}