Characteristics of normal probability curve
Table of Contents
Table of Contents
A normal probability curve, also known as a Gaussian curve or bell curve, is a common statistical distribution that occurs naturally in many real-world phenomena. It is a bell-shaped curve that represents the distribution of data around the mean. This distribution is important to understand as it is commonly used in statistics and data analysis. In this article, we will explore the characteristics of normal probability curve and how it can impact decision-making.
Normal Probability Curve Characteristics can be a complicated subject, and it is easy to feel overwhelmed when trying to understand the concept. Common pain points include confusion surrounding the definition of a normal probability curve, how it is used in different fields, and its relevance to data analysis.
The target of Normal Probability Curve Characteristics is to provide an introduction to the basic statistical concepts behind the normal probability curve. This includes understanding the mean, standard deviation, and the nature of a bell curve.
In summary, Normal Probability Curve Characteristics are an important statistical concept that affects our daily lives. Understanding what a normal probability curve is, how it is used, and how it can impact decision-making can have immense benefits.
What are the Characteristics of Normal Probability Curve?
Normal probability curves have several notable characteristics that make them useful in data analysis. One of these features is that the curve is symmetrical, with the mean, median, and mode all located at the same point. Additionally, the curve follows a bell shape and is continuous, meaning it has no gaps or sudden jumps in the data. Lastly, the curve is asymptotic, which means it approaches but does not touch the x-axis, indicating that there is always a possibility of outliers or extremes in the data.
I work in a data analysis team for a marketing firm, and we frequently use the normal probability curve to understand the performance of our marketing campaigns. For example, we use the normal curve to identify which campaigns have the strongest performance, and we use the mean and standard deviation to understand the variance and distribution of our results.
How to Use Normal Probability Curve Characteristics?
The normal probability curve can be used in a wide variety of fields, as it is a common statistical distribution that represents many natural phenomena. For example, it is often used in finance, healthcare, and engineering disciplines. Understanding the characteristics of the normal probability curve can help individuals make more informed decisions regarding data analysis and statistical inference.
One example of how normal probability curve characteristics can be used is in healthcare. A physician might use the curve to better understand the distribution of patient blood glucose levels. By understanding the mean and standard deviation of blood glucose levels in a population, the physician can better diagnose and treat diabetic patients.
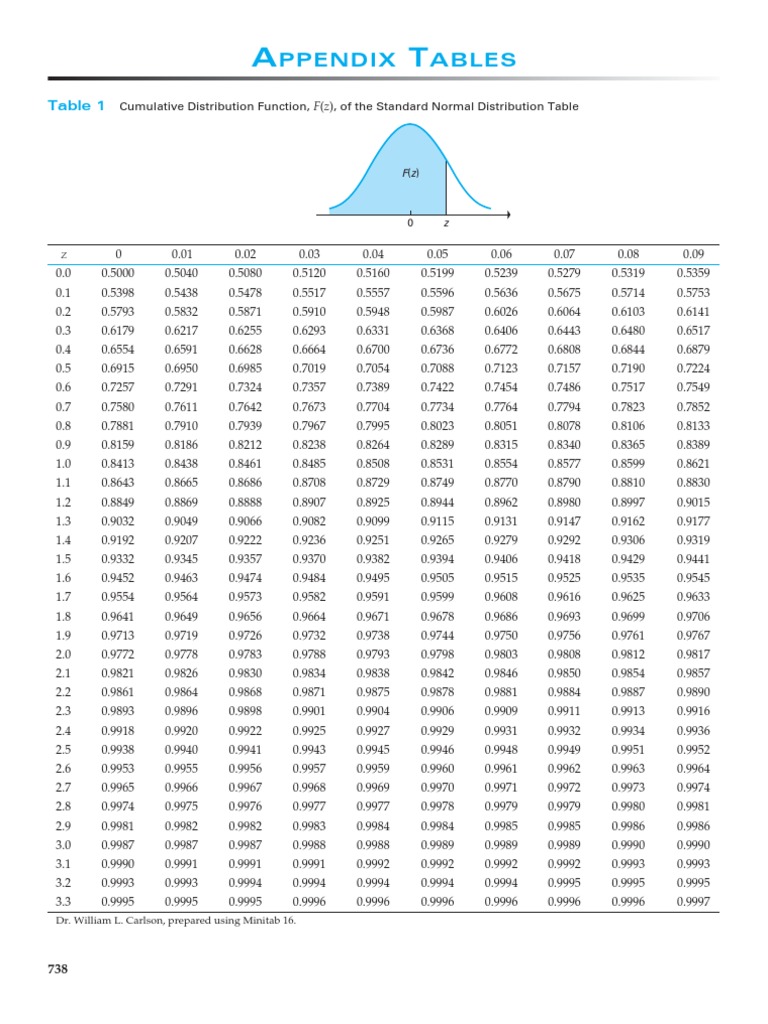
What is the Area Under the Normal Probability Curve?
The area under the normal probability curve is an important statistical concept that can be used to make predictions about the data. For example, if we know the area under the curve, we can calculate the probability of certain outcomes occurring. The area under the curve can be calculated using calculus or statistical software, and it is often used to understand the behavior of a dataset or population.
In our marketing example, we might use the area under the curve to identify which campaigns have the highest probability of generating a high ROI. By understanding the probability of success for each campaign and analyzing the area under the curve, we can optimize our budget and resources for maximum ROI.
What is the Central Limit Theorem?
The central limit theorem is a statistical principle that states that as the sample size of data increases, the data will become more normally distributed around the mean. This means that even if the underlying population is not normally distributed, a large sample size will create a normal distribution. This principle is important because it allows us to make inferences about a population based on a sample.
The central limit theorem is often used in hypothesis testing and statistical inference. For example, if we want to know if the mean height of individuals in a population is significantly different from a certain value, we can use the central limit theorem to create a distribution and perform hypothesis testing.
Question and Answer
Q: What is the difference between a normal probability curve and a standard normal curve?
A: A normal probability curve represents any normal distribution, while a standard normal curve is a specific normal distribution with a mean of 0 and a standard deviation of 1.
Q: Can a normal probability curve have negative values?
A: Yes, a normal probability curve can extend to negative values if the data being analyzed has a negative mean.
Q: How is the normal probability curve used in hypothesis testing?
A: The normal probability curve is used to create a distribution of a sample and perform hypothesis testing to determine if the sample is representative of the population.
Q: What is the relationship between the normal probability curve and the binomial distribution?
A: The binomial distribution can be approximated by the normal probability curve under certain conditions. Specifically, if the sample size is large enough and the probability of success is not too close to 0 or 1, the binomial distribution can be approximated by the normal curve.
Conclusion of Normal Probability Curve Characteristics
The normal probability curve is a powerful statistical tool that represents the distribution of data around the mean. By understanding the characteristics of this curve, individuals can gain valuable insights and make more informed decisions based on data analysis. Whether you are in the field of finance, healthcare, or marketing, understanding this curve can help you optimize your resources, avoid outliers, and make predictions about the data.
Gallery
PPT - COMMONLY USED PROBABILITY DISTRIBUTION PowerPoint Presentation

Photo Credit by: bing.com / probability distribution curve normal ppt commonly used powerpoint presentation
Normal Probability Distribution Curve. | Download Scientific Diagram

Photo Credit by: bing.com / probability
Characteristics Of Normal Probability Curve

Photo Credit by: bing.com / probability characteristics
Characteristics Of Normal Probability Curve

Photo Credit by: bing.com / delphi brainstorming curve probability nominal pqm technique
Image - Normal Curve Probability.jpg | What I Learned Wiki | FANDOM

Photo Credit by: bing.com / probability iq statistics normality mind sigma