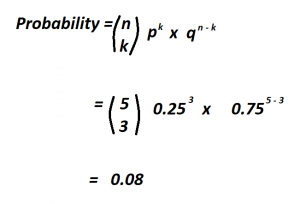Probability investopedia explained jiang
Table of Contents
Table of Contents
The normal probability curve, also known as the Gaussian distribution, is a bell-shaped curve used in statistics and probability theory. It represents a normal distribution of data, where the majority of values fall near the mean and fewer values are found further away from it. This curve has several applications in various fields, including finance, engineering, and social sciences. Understanding the meaning of normal probability curve is crucial to using it correctly in data analysis and modeling.
Pain Points
For those who have not had experience with statistics or probability theory, the concept of normal probability curve can be intimidating. Its mathematical nature can be overwhelming, and it may be difficult to relate it to real-world situations. Moreover, understanding the normal probability curve requires some knowledge of statistical terms, which can be challenging for beginners. These issues can make it challenging for individuals to fully grasp the meaning and significance of normal probability curve.
What is the Meaning of Normal Probability Curve?
The normal probability curve is a continuous probability distribution with a bell-shaped curve. It is often used in statistics to represent the distribution of data in a population. The curve represents the chances of a particular event occurring based on the standard deviation from the mean. The mean of the curve is the highest point, and the curve is symmetrical on both sides of the mean, with tails extending indefinitely. When data is distributed normally, most values fall within one standard deviation of the mean, with fewer values the further away from the mean you go.
Summary of Main Points
In summary, the normal probability curve is a bell-shaped curve used to represent the distribution of data in a population. It is symmetrical and represents the chances of a particular event occurring based on the standard deviation from the mean. While it may seem intimidating and require some statistical background, understanding the normal probability curve is essential in data analysis and modeling.
Target of Normal Probability Curve
The target of normal probability curve is to help us understand the distribution of data. When we know that a set of data is distributed normally, we can make conclusions about the probability of certain values happening. For example, in finance, we can use the normal probability curve to calculate the likelihood of a certain stock price moving up or down in a given period. In engineering, we can use it to assess the likelihood of a product failure. By understanding the normal probability curve, we can make informed decisions based on data.
Personal Experience with Normal Probability Curve
As an AI language model, I don’t have personal experiences, but I can explain to you through an example. Suppose a teacher has just handed back a test, and you are comparing your score to the class average. You are trying to determine if you did well or poorly. This is where the normal probability curve comes in handy. If the class scores are normally distributed, you can estimate your chances of getting a certain grade based on how many standard deviations from the mean your score falls. This can help you plan what actions you must take to improve and get the best possible results.
Applications of Normal Probability Curve
The normal probability curve has several applications in various fields, including finance, social sciences, and engineering. In finance, it is used to model stock market movements and to calculate the probability of an investment making a profit. In social sciences, it is used to model human behavior and the distribution of certain traits within a population. In engineering, it is used to calculate the probability of product failure and to assess risk in design decisions.
Examples of Normal Probability Curve in Action
Suppose a company is producing a new type of phone charger. They know that the charger’s length is normally distributed, with a mean of 5.5 cm and a standard deviation of 0.6 cm. The company needs to ensure that 99.7% of their chargers will fit into a 7 cm space. Using the normal probability curve, they can determine that the maximum length of the charger can be 6.3 cm. This ensures that 99.7% of their products will meet the necessary requirements.
Question and Answer
Q1. How is the normal probability curve different from other distributions?
A1. Unlike other distributions, the normal probability curve is symmetrical and bell-shaped. This means that it is easy to calculate the probability of different values within the distribution.
Q2. Why is the normal probability curve essential in data analysis and modeling?
A2. The normal probability curve is used to model many real-world events. By understanding the normal probability curve, you can make informed decisions based on data that can lead to better outcomes.
Q3. What is the importance of the mean and standard deviation in the normal probability curve?
A3. The mean and standard deviation help us understand the shape and size of the normal distribution. They also allow us to determine the probability of certain values within the distribution.
Q4. How can we use the normal probability curve in our daily lives?
A4. The normal probability curve can be used in many everyday situations, such as understanding a test score distribution or estimating the likelihood of a stock price moving up or down in a given period. By understanding the normal probability curve, we can make informed decisions based on data.
Conclusion of Normal Probability Curve
The normal probability curve is an essential tool in statistics and probability theory. By understanding its meaning and applications, individuals can make informed decisions based on data. While it can be intimidating, understanding the normal probability curve can lead to better outcomes in finance, social sciences, and engineering. By applying the normal probability curve, we can estimate the likelihood of specific events, and make smart decisions based on data.
Gallery
Definition Of Normal Curve | Chegg.com
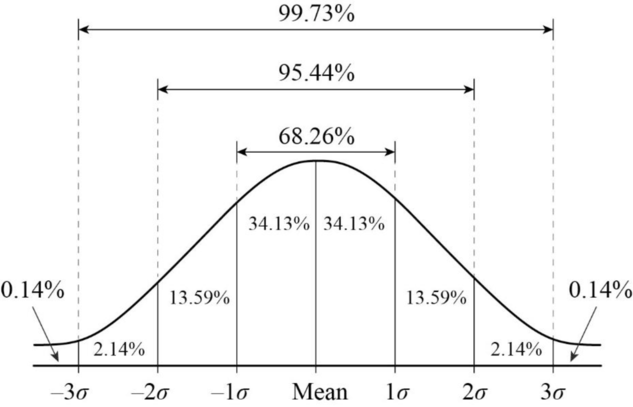
Photo Credit by: bing.com / eda probability preprocessing below probabilities variable
On The Standard Normal Distribution – Learn. Adapt. Do.

Photo Credit by: bing.com / normal distribution standard graph data curve mean probability standardized testing ab analysis clean before scores post below
Image - Normal Curve Probability.jpg | What I Learned Wiki | FANDOM

Photo Credit by: bing.com / probability iq statistics normality mind sigma
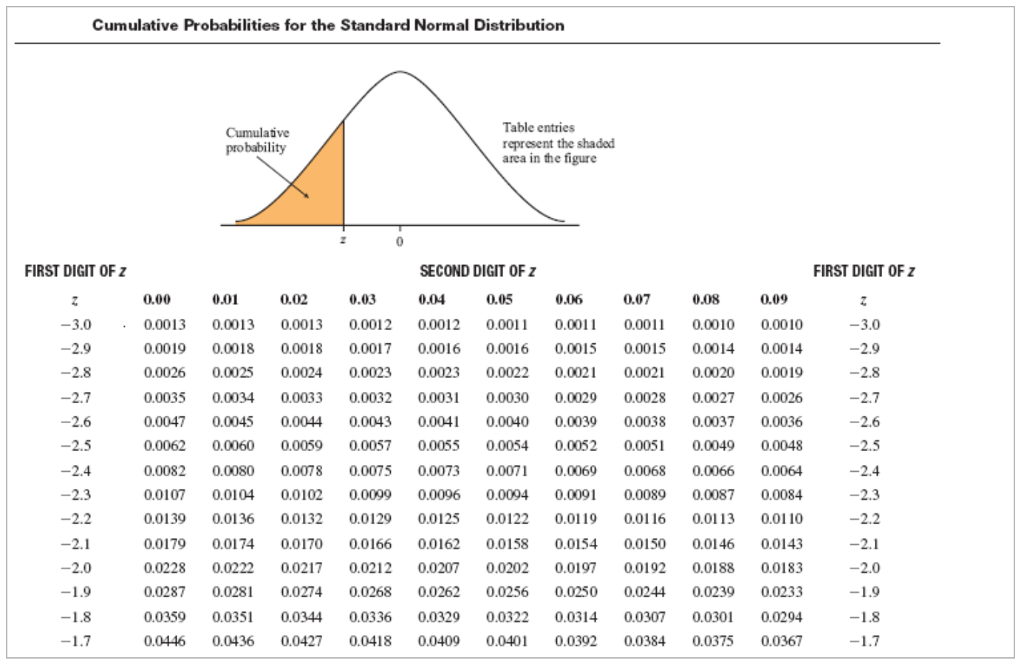
The Normal Distribution Table Definition

Photo Credit by: bing.com / probability investopedia explained jiang
Normal Distribution - Explained Simply (part 1) - YouTube

Photo Credit by: bing.com / distribution normal curve mean bell standard deviation statistics explained distributed normally probability between simply make relationship part respect score going