Solved question 7 assume that a procedure yields a binomial
Table of Contents
Table of Contents
Are you struggling to understand the concept of binomial probability and how to use the binomial probability formula? If so, you are not alone! Many people find this topic confusing and difficult to grasp. But fear not, in this article, we will break down the binomial probability formula and explain how to use it in everyday scenarios.
Calculating probability can be a pain point for many students and professionals alike. The idea of using formulas and equations to determine a likelihood can seem daunting, especially if math is not your strong suit. However, understanding the binomial probability formula is essential in fields such as finance, science, and engineering, where predicting outcomes and assessing risks are crucial.
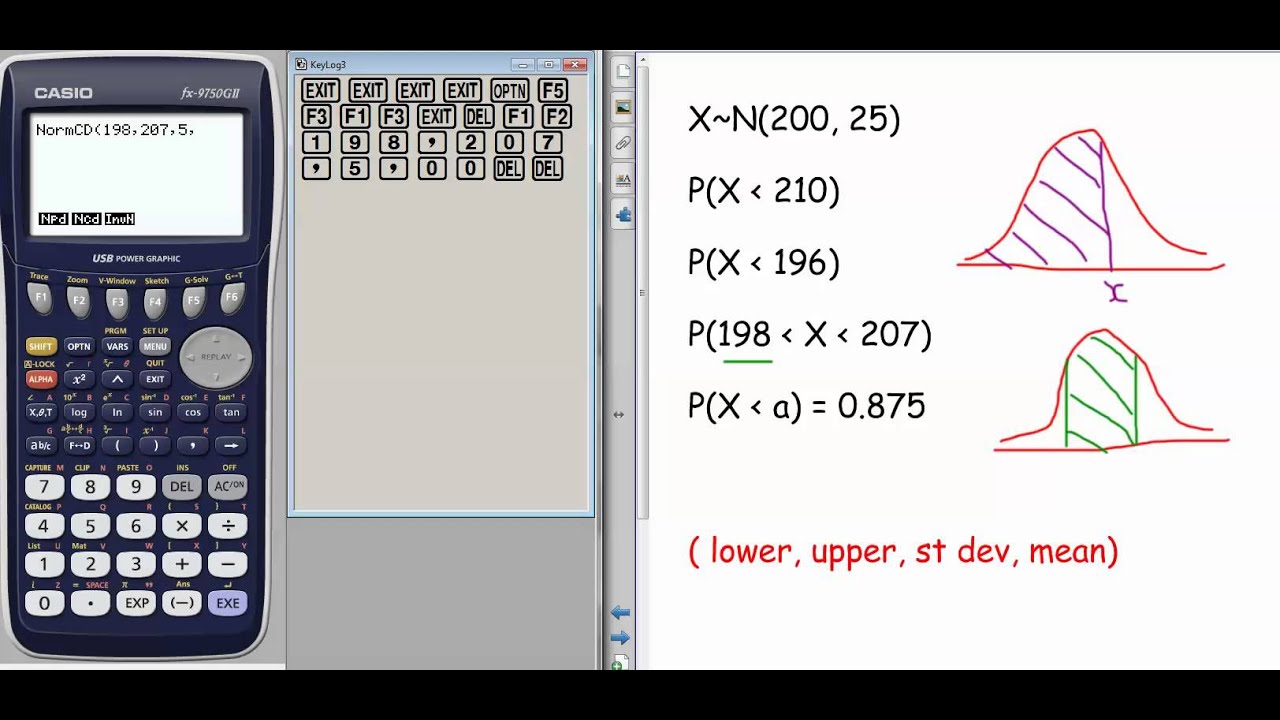
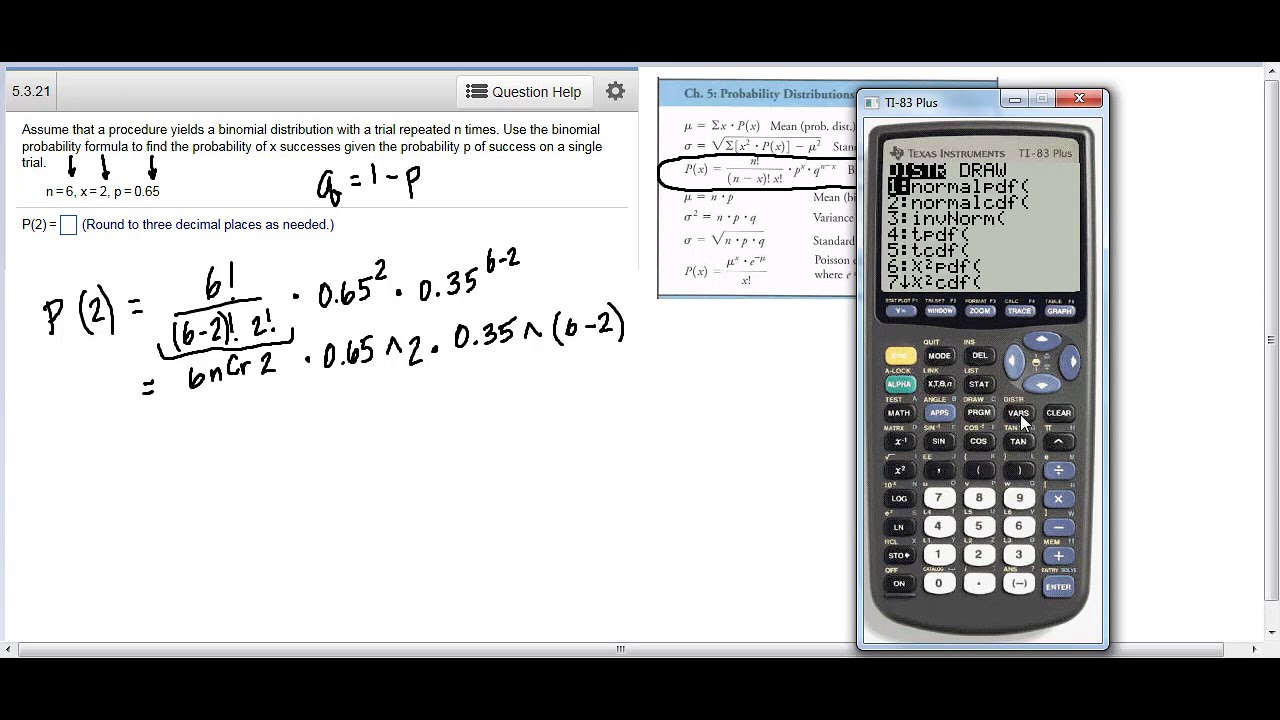
The binomial probability formula is used to determine the probability of getting a certain number of successes in a specific number of trials. It involves calculating the probability of a single event and then multiplying it by the number of trials. The formula is expressed as: P(x) = (nCx) * p^x * q^(n-x), where n is the total number of trials, x is the number of successful events, p is the probability of success on a single trial, and q is the probability of failure on a single trial.
In summary, the binomial probability formula allows us to calculate the probability of a given number of successes in a specific number of trials. By understanding this formula, we can predict outcomes and assess risks in various fields, making it a valuable tool to have in our problem-solving arsenal.
How To Use The Binomial Probability Formula in Real Life
As a data analyst, I recently used the binomial probability formula to predict the likelihood of a customer being a repeat buyer. By analyzing past buying behavior, we were able to determine the probability of a customer purchasing again based on the number of previous purchases. This allowed us to create targeted marketing strategies to encourage repeat business.
Another example of how to use the binomial probability formula is in sports. For instance, a basketball coach may use it to predict the probability of their team winning a certain number of games in a season. By analyzing past games and tracking performance, they can use the binomial probability formula to determine the likelihood of reaching their goal and adjust their strategies accordingly.
Understanding the Components of the Binomial Probability Formula
Let’s break down the different components of the binomial probability formula:
n
The “n” in the formula refers to the total number of trials or events that will take place. For example, if you are flipping a coin ten times, then n = 10.
x
The “x” in the formula represents the total number of successful events. For example, if you are flipping a coin and want to know the probability of getting 5 heads, then x = 5.
p
The “p” in the formula stands for the probability of a single event being successful, such as the probability of flipping a heads on a coin. This number is usually expressed as a decimal.
q
The “q” represents the probability of a single event being a failure. This number is calculated by subtracting the probability of success (p) from 1.
Frequently Asked Questions About How To Use The Binomial Probability Formula
Q: What if I have more than two outcomes?
A: The binomial probability formula is only used when there are two outcomes (success or failure) for a given event. If you have more than two outcomes, you will need to use a different formula, such as the multinomial probability formula.
Q: Why is the binomial probability formula important?
A: The binomial probability formula is essential in various fields where predicting outcomes and assessing risks are crucial. It allows us to calculate the probability of a given number of successful events in a specific number of trials.
Q: How do I calculate the probability of success on a single trial?
A: To calculate the probability of success on a single trial, you can divide the number of successful events by the total number of events. For example, if you flip a coin ten times and it lands on heads six times, the probability of success on a single trial would be 0.6.
Q: Can the binomial probability formula be used in financial forecasting?
A: Yes, the binomial probability formula can be used in financial forecasting to determine the probability of a particular outcome based on a set of variables. For example, it could be used to calculate the probability of a stock price rising or falling based on past performance and market trends.
Conclusion of How To Use The Binomial Probability Formula
The binomial probability formula may seem intimidating at first, but by breaking down its components and understanding its usage, you can apply it to real-life scenarios. Whether you are a data analyst, sports coach, or finance professional, the binomial probability formula is a valuable tool to have in your problem-solving arsenal.
Gallery
How To Calculate Binomial Probability.
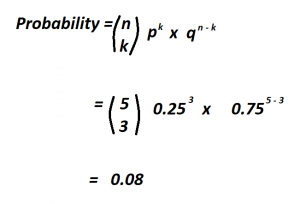
Photo Credit by: bing.com / probability binomial calculate exactly
PPT - Binomial Probability Formula PowerPoint Presentation - ID:2635610

Photo Credit by: bing.com / binomial probability
Binomial Probability Distribution Tutorial

Photo Credit by: bing.com / binomial probability formulas calculate successes onlinemathlearning trials tosses fraction bernoulli roll
Solved Question 7 Assume That A Procedure Yields A Binomial | Chegg.com
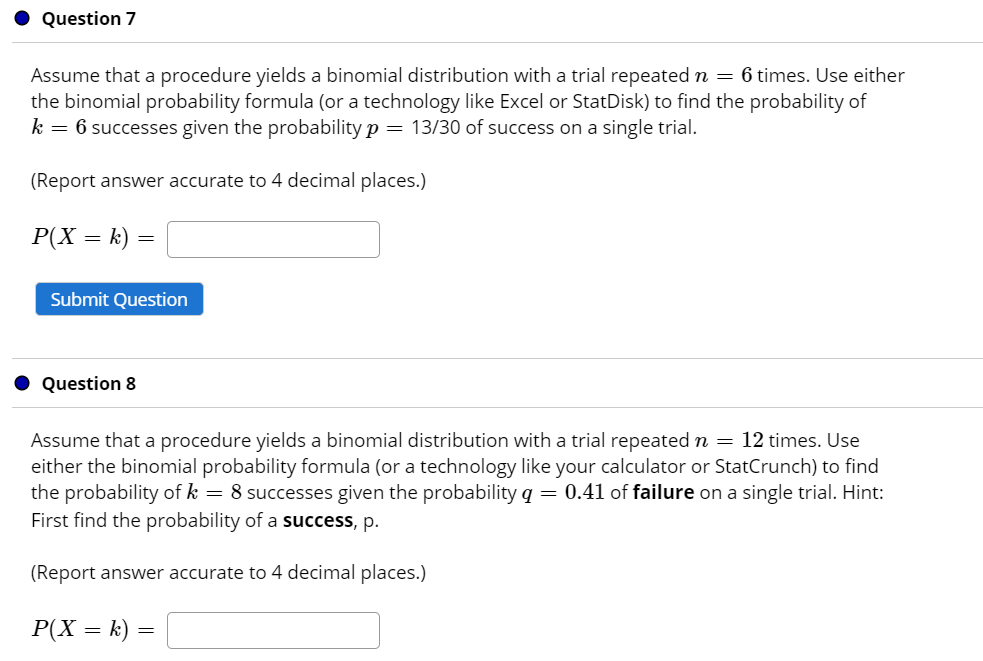
Photo Credit by: bing.com / yields assume solved binomial repeated transcribed
PPT - The Binomial Distribution PowerPoint Presentation, Free Download

Photo Credit by: bing.com / binomial distribution formula ppt trials probability general powerpoint presentation number