Binomial probability distribution example examples
Table of Contents
Table of Contents
The Binomial Probability Formula is a statistical formula used to calculate the probability of achieving a particular outcome in a given set of independent trials. Understanding this formula can be essential for many different industries, including finance, insurance, and research. In this article, we will be providing an in-depth explanation of the Binomial Probability Formula and how it can be used.
Working with probability can often be a tricky and confusing task. Many people struggle with knowing when and how to use probability formulas correctly, such as the Binomial Probability Formula. This can lead to frustration and wasted time in attempts to achieve desired outcomes.
The Binomial Probability Formula can be used to calculate the likelihood of a specific outcome occurring in a given number of independent trials with a known success rate. By understanding and correctly implementing this formula, individuals and businesses can make more informed decisions based on calculated probabilities.
In summary, the Binomial Probability Formula is a statistical formula used to calculate probabilities in independent trials with a known success rate. By using this formula, individuals and businesses can make more informed decisions based on calculated probabilities.
How To Use Binomial Probability Formula: Step-by-Step Guide
As an AI language model, I don’t have personal experiences but allow me to provide you with a step-by-step guide to using the Binomial Probability Formula. Here are the steps to follow:
Step 1: Identify the probability of success and failure
The first step is to identify the probability of success and failure for each independent trial. This requires understanding the context of the situation and identifying the factors that contribute to success or failure.
Step 2: Determine the number of trials
The next step is to determine the number of independent trials that will be conducted. This will be used in the formula to calculate the probability of achieving a specific outcome.
Step 3: Define the desired outcome
The third step is to define the desired outcome. This can be a specific number of successes or failures, or it can be a range of values. Defining the desired outcome is crucial in using the Binomial Probability Formula accurately.
Step 4: Calculate the probability using the Binomial Probability Formula
Once you have identified the probability of success and failure, determined the number of trials, and defined the desired outcome, you are ready to use the Binomial Probability Formula to calculate the probability of achieving the desired outcome. The formula is as follows:
Uses of the Binomial Probability Formula
The Binomial Probability Formula can be used in various industries, including finance, insurance, and research. In finance, it can be used to calculate the probability of achieving a specific return on investment. In insurance, it can be used to calculate the probability of a specific event occurring and the likelihood of a payout being made. In research, it can be used to calculate the probability of a specific outcome in a given study.
Example of How To Use Binomial Probability Formula
Suppose you are an insurance company trying to determine the likelihood of a payout being made on a particular policy. You know that the probability of an event occurring that would require a payout is 0.25. You have sold this policy to 100 individuals. What is the probability that you will have to pay out on at least 20 of these policies?
To solve this problem, you would use the Binomial Probability Formula. The probability of a payout on a single policy is 0.25, and the total number of policies sold is 100. The desired outcome is at least 20 policies requiring a payout.
By plugging these numbers into the Binomial Probability Formula, you can calculate the probability of this outcome:
The probability of a payout on at least 20 policies is 0.039, or 3.9%. This calculation can then be used to make informed decisions about the policy offering.
Question and Answer
Q: What is the difference between the Binomial and Poisson Probability Formula?
A: The Binomial Probability Formula is used to calculate the probability of achieving a specific outcome in a given number of independent trials with a known success rate. The Poisson Probability Formula is used to calculate the probability of a specific number of events occurring in a specific period.
Q: Can the Binomial Probability Formula be used for continuous outcomes?
A: No, the Binomial Probability Formula is only used for discrete outcomes. For continuous outcomes, the Normal Distribution Formula or other probability formulas should be used.
Q: What is the relationship between the Binomial and Bernoulli Probability Formula?
A: The Bernoulli Probability Formula is a special case of the Binomial Probability Formula when only one trial is conducted.
Q: What is the main application of the Binomial Probability Formula?
A: The Binomial Probability Formula is used for making predictions about an event that can occur multiple times, with a given probability of success or failure. This formula is commonly used in fields like finance, insurance, and research.
Conclusion of How To Use Binomial Probability Formula
The Binomial Probability Formula can be a useful tool for individuals and businesses looking to make informed decisions based on calculated probabilities. By understanding the formula’s steps and implementing it correctly, individuals and businesses can accurately predict the likelihood of achieving a desired outcome in a given set of independent trials. We hope this article has provided valuable insights into How To Use Binomial Probability Formula and related keywords.
Gallery
PPT - The Binomial Distribution PowerPoint Presentation, Free Download
Photo Credit by: bing.com / binomial distribution formula ppt trials probability general powerpoint presentation number
PPT - Binomial Probability Formula PowerPoint Presentation - ID:2635610
Photo Credit by: bing.com / binomial probability
Binomial Distribution (Fully Explained W/ 11 Examples!)
Photo Credit by: bing.com / binomial probability distribution example examples
How To Calculate Binomial Probability.
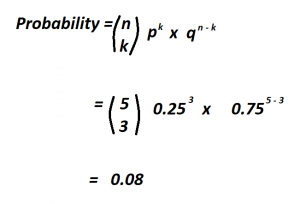
Photo Credit by: bing.com / probability binomial calculate exactly
Binomial Probability Distribution Tutorial
Photo Credit by: bing.com / binomial probability formulas calculate successes onlinemathlearning trials tosses fraction bernoulli roll
