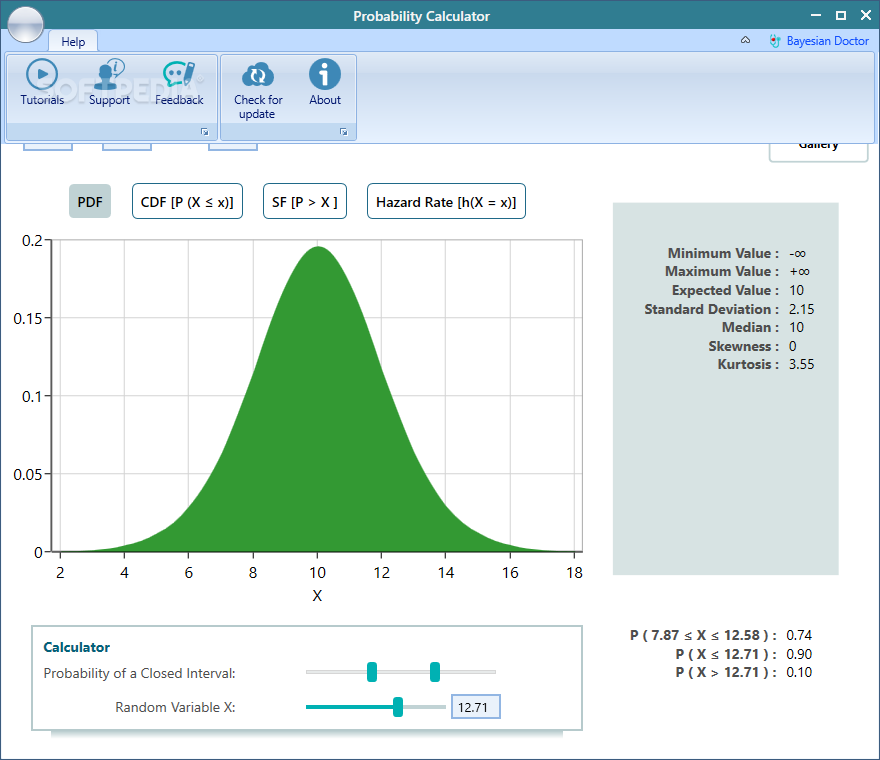
Construct a probability distribution calculator
Table of Contents
Table of Contents
As you dive into the world of probability, you will come across a familiar term called “binomial probability.” This concept is crucial in understanding probability and statistics, and it is essential to master to make meaningful conclusions in real-world scenarios. In this blog post, we will delve deeper into how to solve binomial probability and its significance in statistics.
Pain Points of Binomial Probability
Many find binomial probability challenging to comprehend. Moreover, this problem becomes more complicated when the experiment model changes. For instance, it is not easy to handle binomial probability experiments with big numbers. Moreover, computing binomial probability takes a lot of effort without knowing the correct formula.
Target of How To Solve Binomial Probability
One of the essential aspects of understanding binomial probability is knowing when to use it. Binomial probability is used when an experiment has two possible outcomes of either success or failure. This blog post will help you understand the concept of binomial probability, provide techniques to solve it, and guide you to appropriate resources for further skills development.
Summary of Main Points
Binomial probability is a crucial part of statistics and probability. It can be challenging to comprehend due to its underlying complexity, especially when the experiments’ model changes. This blog post aims to provide insights into the target of binomial probability, discuss the pain points related to binomial probability, and offer techniques to solve it with ease.
How To Solve Binomial Probability - Techniques and Personal Experience
Recently, I had to solve a binomial probability problem in my data analytics course project. Although I had studied the concept in class, I found myself stuck on the problem and lost confidence in my ability. However, with the help of a tutor and some practice, I managed to solve the problem, which helped me gain confidence in my abilities.
The binomial probability formula is a useful tool when faced with such problems. The formula is:
Where:
- p is the probability of success
- q is the probability of failure (q=1-p)
- n is the number of trials
- x is the number of successes
The formula is instrumental, especially when solving binomial probability problems using combinations and permutations. Another useful tip is to break the problem down into smaller, more manageable parts. This approach helps you avoid mistakes and uncover any hidden assumptions you might have made.
Binomial Probability Distribution - Resources and Examples
Several resources provide assistance with binomial probability distribution problems. Textbooks and online courses can give you an in-depth understanding of the concept and its application. In addition, online probability calculators save time and help avoid errors when solving such problems. The following example showcases how to calculate binomial probability:
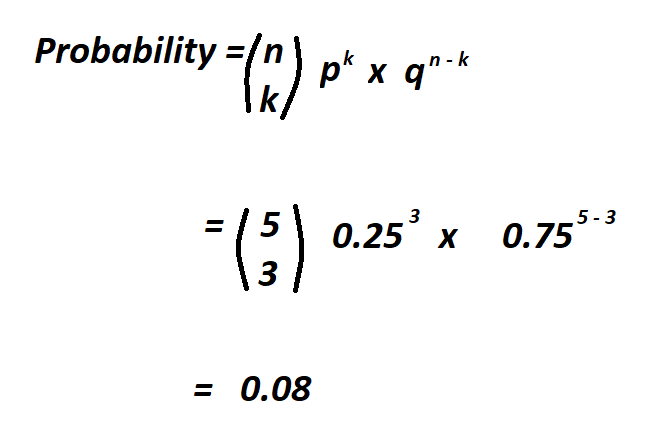Suppose you want to calculate the probability of getting a head four times in a row when tossing a coin. Assuming the probability of success (getting a head) is 0.5, the probability using the binomial probability formula is:
P(X=4) = (4C4) * 0.5^4 * (1 - 0.5)^(4-4) = 0.0625
Advanced Techniques of Solving Binomial Probability
While basic techniques are sufficient to solve most binomial problems, several advanced techniques can be useful when dealing with more complex situations. One such technique is the application of the Poisson distribution. The Poisson distribution is used when the number of trials is large, and the probability of success is small. This distribution takes into account the variance of the experiment, making it more accurate when dealing with large values.
Applications of Binomial Probability
Binomial probability has several applications in everyday life, including quality control, survey sampling, and medical testing. In manufacturing, binomial probability can help determine the average number of defects in a batch of products. In medicine, it can be used to determine the number of patients who respond to a new treatment. In survey sampling, it can be used to determine the number of people who support a political candidate.
Question and Answer
Q: What is binomial probability used for?
A: Binomial probability is used when an experiment has two possible outcomes of either success or failure.
Q: When is the Poisson distribution used?
A: The Poisson distribution is used when the number of trials is large, and the probability of success is small.
Q: What is the binomial probability formula?
A: The binomial probability formula is: P(X=x) = (nCx) * p^x * (1 - p)^(n-x).
Q: What are some applications of binomial probability?
A: Quality control, survey sampling, and medical testing are some applications of binomial probability.
Conclusion of How To Solve Binomial Probability
In conclusion, binomial probability is an essential concept in understanding probability and statistics. It can be challenging to comprehend, but with the right techniques and practice, it is possible to solve complex problems. We hope this blog post has provided valuable insights into how to solve binomial probability and its applications in everyday life.
Gallery
Binomial Probability Distribution Tutorial
Photo Credit by: bing.com / binomial probability formulas calculate successes onlinemathlearning trials tosses fraction bernoulli roll
PPT - Binomial Probability Distribution 1. The Experiment Must Have A
Photo Credit by: bing.com / binomial probability distribution formula experiment trials fixed number method must ppt powerpoint presentation qn px slideserve
How To Calculate Binomial Probability.
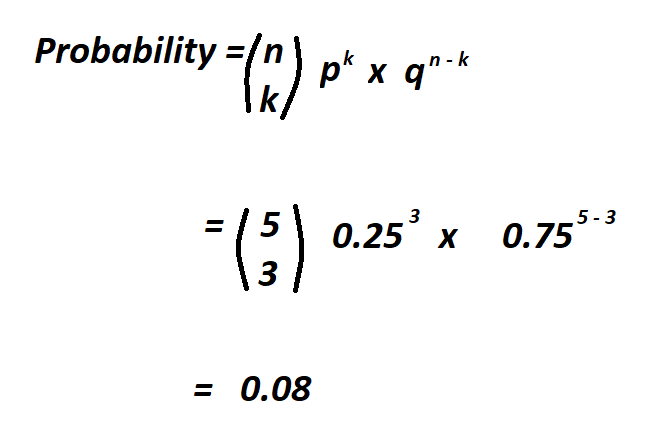
Photo Credit by: bing.com / probability binomial calculate exactly
Binomial Distribution (Fully Explained W/ 11 Examples!)
Photo Credit by: bing.com / binomial probability distribution example examples
Construct A Probability Distribution Calculator - Research Topics
Photo Credit by: bing.com / binomial probability construct probabilities finding
