Cumulative Binomial Probability Formula

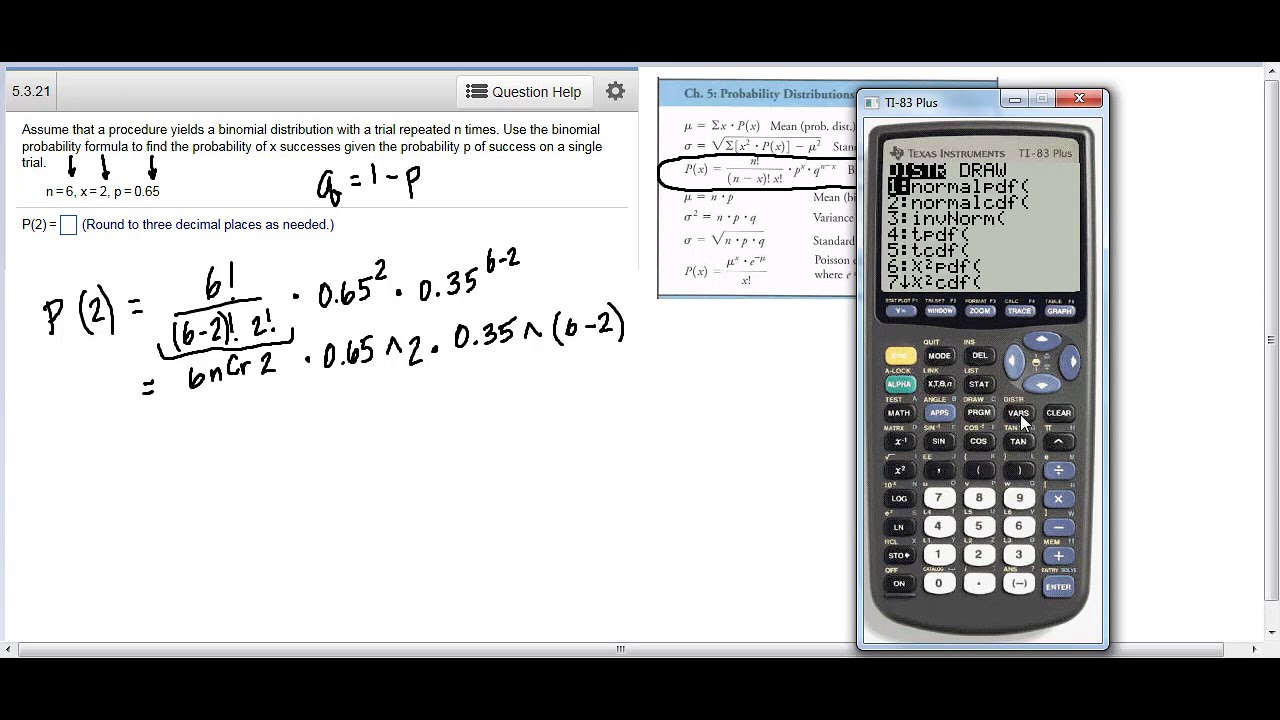
Binomial probability references

Table of Contents

The Cumulative Binomial Probability Formula is an essential concept in many fields, including statistics, economics, and business. Understanding this formula can help you make more informed decisions in your industry and improve your overall productivity.

Whether you are a business owner trying to forecast sales, a researcher developing experiments in science, or a student just trying to understand mathematics better, the Cumulative Binomial Probability Formula can be challenging to grasp. The primary difficulties people face when tackling this formula include understanding the probability of success and how it changes as trials increase, along with determining the number of potential outcomes.

Simply put, the Cumulative Binomial Probability Formula is a statistical function that measures the probability of a series of independent, identical events occurring and the chance of achieving a particular number of successes in a given number of tries.

In short, the formula measures the likelihood of obtaining more than X number of successes in a given number of trials, where X is any integer. This formula can help us make important decisions about resource allocation, risk management, and other business-related decisions.

Cumulative Binomial Probability Formula Explained

When I first learned about the Cumulative Binomial Probability Formula, I remember feeling overwhelmed. However, once I recognized that this formula only required basic algebraic manipulation and a few simple calculations, it became much easier to understand.

The formula calculates the probability of obtaining a certain number of successes (x) in a particular number of trials (n) and is expressed as follows:

Where:

• p is the probability of success on any given trial
• n is the number of trials
• x is the number of successes we want to measure
• (1-p) is the probability of failure on any given trial

Applications in Business

Understanding the Cumulative Binomial Probability Formula can be super beneficial when trying to solve or forecast quantitative business problems, including:

• Forecasting the number of orders if you have an estimated probability of a sale
• Predicting the number of sales in a given period if you know your conversion rate
• Calculating the probability that a certain number of products in production will pass quality control tests

How To Apply It

To apply the Cumulative Binomial Probability Formula in any of the above applications, first define the probability of success, the number of trials you will conduct, and the threshold of success you want to measure.

For example, suppose you know that your sales team’s average conversion rate is 30%, and you want to forecast how many sales you should expect from a list of 100 leads. You can use the Cumulative Binomial Probability Formula to calculate the number of outcomes you can expect within a particular range.

Example Calculation

p = 0.3, n = 100, x = any integer

If we solve this formula for x = 0 (no sales), we get:

According to our calculation, there is a 0.0063 or 0.63% chance that no sales will happen with those 100 leads. Similarly, we can solve this formula for x = 10 (10 sales) to calculate the probability of 10 sales.

Question and Answer

What is the difference between Binomial Distribution and Cumulative Binomial Probability?

The Binomial Distribution formula is the formula used to calculate the probability of obtaining exactly x successes in n trials, while Cumulative Binomial Probability is the probability of at least x successes in n trials.

When is the Cumulative Binomial Probability formula used?

The Cumulative Binomial Probability formula is used to calculate the probability of obtaining a specific range of successes in n trials.

What is the probability that if we flip a coin ten times, we will get at least five tails and five heads?

We can use the Cumulative Binomial Probability formula for this. i.e.,

p = 0.5 (because this is a coin flip where the outcome of getting a tail is equal to getting a head), n = 10, x = at least one occurrence of five tails and five heads.

By plugging this into the formula, we can find the exact probability, which is 50.0%.

What is the main application of the Cumulative Binomial Distribution in business analysis?

The main application of the Cumulative Binomial Probability formula in business analysis is to perform statistical analyses to help forecast future resource allocation, risk management, and decision-making.

Conclusion of Cumulative Binomial Probability Formula

The Cumulative Binomial Probability Formula is a powerful tool to calculate the probability of a particular outcome in a series of defined trials. Its applications are vast and generally applicable across many industries and fields. Understanding this formula can help you make better resource allocation decisions, forecast sales and production numbers, and make informed decisions in risk management.

Gallery

Cumulative Binomial Probability - YouTube

_{^{Photo Credit by: bing.com / binomial probability cumulative}}

Binomial Probability Of Success

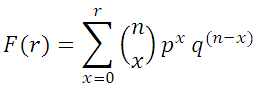
_{^{Photo Credit by: bing.com / binomial distribution probability cdf cumulative acceptance equation success sample where example function appspot}}

Extreme Precision Binomial Probability Calculator

_{^{Photo Credit by: bing.com / binomial probability references}}

Binomial Distribution Calculator - Binomial Probability Calculator

_{^{Photo Credit by: bing.com / binomial cdf distribution cumulative function probability formula calculator calculations}}

Cumulative Binomial Distribution [Year 1 Maths (Stats)] - YouTube

_{^{Photo Credit by: bing.com / binomial cumulative}}