Solved a construct a binomial probability distribution
Table of Contents
Table of Contents
Have you ever wondered about the chances of a certain event happening multiple times in a set number of trials? This is where the concept of Constructing A Binomial Probability Distribution comes in. Understanding this concept is important for decision makers and researchers alike, as it can help in predicting future outcomes of certain experiments and trials.
Constructing A Binomial Probability Distribution can be a bit overwhelming for those who are not well-versed in statistics. The idea of calculating probabilities and understanding the parameters might seem like a daunting task. However, having a basic understanding of Binomial Probability Distribution can be very useful in many real-world scenarios.
The target of Constructing A Binomial Probability Distribution is to calculate the probability of a certain number of successes in a set number of trials with a given probability of success. For example, if we know the probability of a basketball player making a free throw and we want to know the likelihood of them making two out of three shots, Binomial Probability Distribution can help us with the calculation.
In summary, Constructing A Binomial Probability Distribution is the process of calculating the probability of a certain number of successes in a set number of trials with a given probability of success. Understanding this concept is important for predicting future outcomes and making informed decisions.
Personal Experience with Binomial Probability Distribution
During my undergraduate studies, I was working on a research project that involved studying the behavior of mosquitoes in response to certain stimuli. We conducted experiments where a certain number of mosquitoes were exposed to the stimuli and we noted down the number of mosquitoes that responded positively. We used Binomial Probability Distribution to calculate the probability of a certain number of mosquitoes responding positively in a set number of trials. This helped us in predicting the number of mosquitoes that might respond positively if we conducted the same experiment in different conditions.
Usage of Binomial Probability Distribution in Real Life
Binomial Probability Distribution has various real-life applications. For example, it is commonly used in medical trials to determine the effectiveness of a new drug. It is also used in quality control experiments to determine the probability of defects in a set number of products. Understanding the concept of Binomial Probability Distribution can be useful for decision-making in various industries.
How to Calculate Binomial Probability Distribution?
The formula for calculating Binomial Probability Distribution is as follows:
 Where:
Where:
- P(x) is the probability of x successes in n trials.
- n is the fixed number of trials.
- x is the number of successes.
- p is the probability of success in a single trial.
- q is the probability of failure in a single trial (q = 1 - p).
Example
Suppose we flip a coin 10 times and we want to calculate the probability of getting 6 heads. The probability of getting a head on a single flip is 0.5 and the probability of getting a tail is also 0.5. Therefore, p = 0.5 and q = 1 - p = 0.5. Using the Binomial Probability Distribution formula, we can calculate:
P(6) = (10 choose 6) x (0.5)^6 x (0.5)^4 = 0.205078
Therefore, the probability of getting 6 heads in 10 flips is approximately 0.205 or 20.5%.
FAQs About Binomial Probability Distribution
Q: What is the difference between Binomial Probability Distribution and Poisson Distribution?
A: Both Binomial and Poisson Distributions are used to calculate the probability of certain events. However, Binomial Distribution deals with discrete variables (e.g., number of successes in a set number of trials) while Poisson Distribution deals with continuous variables (e.g., number of events in a certain time frame).
Q: Can Binomial Probability Distribution be used for more than two outcomes?
A: No, Binomial Probability Distribution is only used for two outcomes (success or failure).
Q: What happens if the trials are not independent in Binomial Probability Distribution?
A: If the trials are not independent, then Binomial Probability Distribution cannot be used. Instead, other distributions such as Hypergeometric Distribution or Negative Binomial Distribution might be more appropriate.
Q: Can Binomial Probability Distribution be used for continuous variables?
A: No, Binomial Probability Distribution is only used for discrete variables.
Conclusion of Binomial Probability Distribution
Constructing A Binomial Probability Distribution is an important concept in statistics that can help in predicting future outcomes of certain experiments and trials. It is commonly used in decision-making in various industries such as medicine and quality control. Understanding the formula and parameters of Binomial Probability Distribution can be useful in many real-world scenarios.
Gallery
Solved (a) Construct A Binomial Probability Distribution | Chegg.com

Photo Credit by: bing.com / distribution binomial construct probability parameters given solved
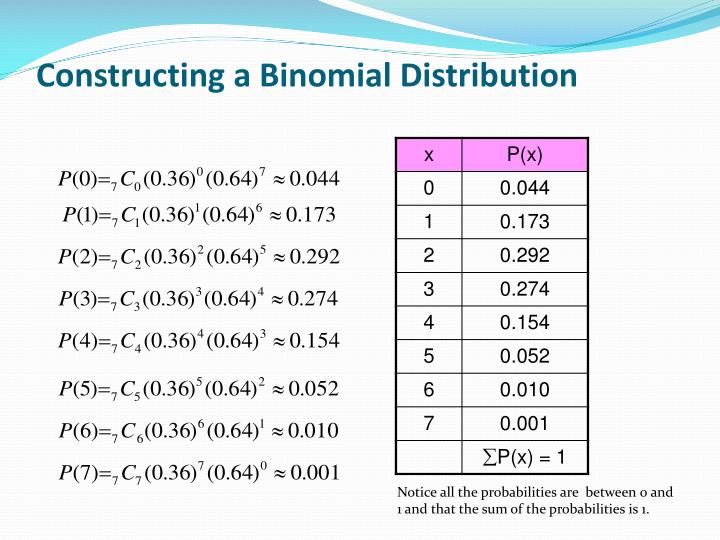
PPT - Binomial Probability Formula PowerPoint Presentation - ID:2635610

Photo Credit by: bing.com / binomial probability distribution formula constructing probabilities ppt powerpoint presentation sum notice between
PPT - 6.1 Binomial Distributions PowerPoint Presentation, Free Download

Photo Credit by: bing.com / binomial distribution distributions probability constructing construct population ppt powerpoint presentation households subscribe parameters cable tv
Solved Use N=6 And P = 0.15 To Complete Parts (a) Through | Chegg.com

Photo Credit by: bing.com / probability distribution binomial construct parts
Solved Use N= 10 And P=0.8 To Complete Parts (a) Through (d) | Chegg.com
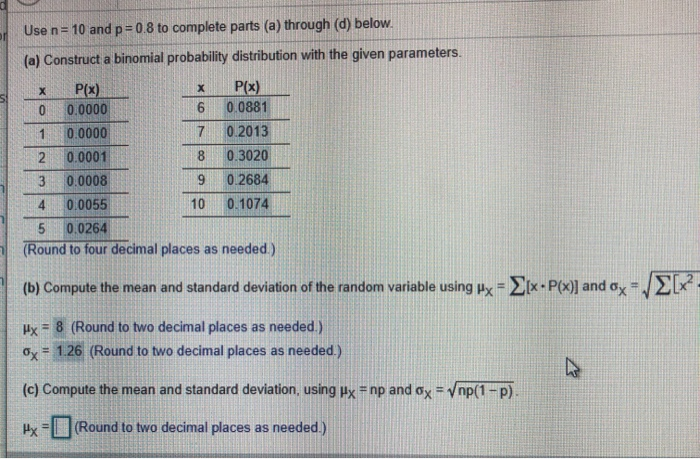
Photo Credit by: bing.com / construct probability binomial distribution