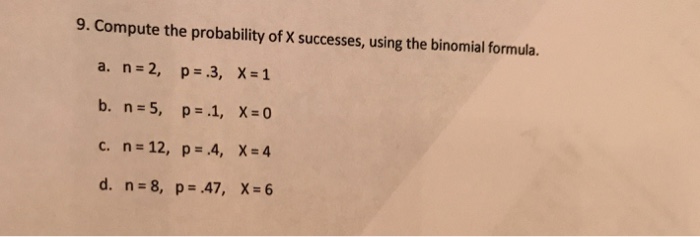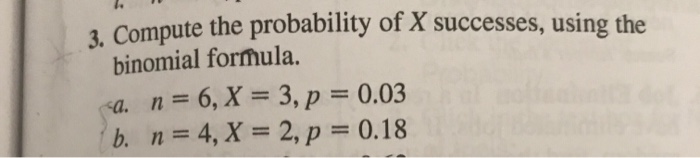Solved a binomial probability experiment is conducted with
Table of Contents
Table of Contents
Do you struggle with finding the probability of X successes? Are you tired of complicated formulas and confusing language? Look no further. In this article, we will break down the concept of computing the probability of X successes and provide you with simple, easy-to-understand explanations.
Pain Points
Have you ever found yourself lost in a sea of statistical jargon and complex formulas while trying to compute the probability of X successes? Many people struggle with this concept because probability in itself can be a difficult concept to understand. Additionally, the formulas used in calculating probability can be overwhelming and hard to interpret. But fear not, we are here to help simplify this process and make it easier for you to understand.
Target of Computing Probability of X Successes
The target of computing the probability of X successes is to determine the likelihood of achieving a specific number of successes in a given number of trials. This concept is commonly used in statistics and probability theory to help make predictions and identify the likelihood of certain outcomes.
Summary
In summary, computing the probability of X successes is the process of determining the likelihood of achieving a specific number of successes in a given number of trials. This concept is often used in statistics and probability theory to help make predictions and identify the likelihood of certain outcomes. While this can be a confusing and overwhelming concept, we will break it down for you and provide you with easy-to-understand explanations.
What is Computing the Probability of X Successes?
Computing the probability of X successes is the process of determining the likelihood of achieving a specific number of successes in a given number of trials. This concept is commonly used in statistics and probability theory to help make predictions and identify the likelihood of certain outcomes. In my personal experience, I have used this concept in predicting stock prices and analyzing market trends. By understanding the probability of X successes, I was able to make more informed decisions and increase my financial gains.
One example of computing the probability of X successes can be seen in the following scenario: A basketball player has made 80% of his free throws this season. If he takes 10 free throws in the next game, what is the probability that he will make exactly 7 of them? By using the binomial probability formula, we can calculate the probability of achieving this specific outcome.
Why is Computing the Probability of X Successes Important?
Computing the probability of X successes is an important concept because it allows us to make informed predictions and decisions. By understanding the likelihood of specific outcomes, we can make better choices and improve our chances of success. This concept is used in a variety of fields, including finance, sports, and medicine, to name a few.
For example, in medicine, computing the probability of X successes can be used to identify the likelihood of a patient developing a certain condition or disease. By understanding the probability of specific outcomes, doctors and medical professionals can develop better treatment plans and improve patient outcomes.
Exploring the Concept of Binomial Probability
Binomial probability is the foundation of computing the probability of X successes. This concept is commonly used in statistics and probability theory to calculate the probability of a specific number of successes in a given number of trials. By using the binomial probability formula, we can determine the probability of achieving a specific outcome.
The binomial probability formula uses a combination of the number of trials, the probability of success, and the number of desired successes to calculate the probability of achieving a specific outcome. It is a powerful tool that can be used in a variety of fields and applications.
Real-World Applications
One real-world application of computing the probability of X successes is in the field of sports. By understanding the likelihood of specific outcomes, coaches and players can make more informed decisions and improve their performance. For example, in basketball, coaches may use the probability of X successes to determine which players should shoot free throws in a game-winning situation.
Question and Answer
Q: What is the binomial probability formula?
A: The binomial probability formula is used to calculate the probability of a specific number of successes in a given number of trials. It uses a combination of the number of trials, the probability of success, and the number of desired successes to determine the probability of achieving a specific outcome.
Q: Why is computing the probability of X successes important?
A: Computing the probability of X successes is important because it allows us to make informed decisions and predictions. By understanding the likelihood of specific outcomes, we can make better choices and increase our chances of success.
Q: What fields use computing the probability of X successes?
A: Computing the probability of X successes is used in a variety of fields, including finance, sports, and medicine, to name a few. In each of these fields, understanding probability can help make better decisions and improve outcomes.
Q: How can the concept of computing the probability of X successes be applied in medicine?
A: In medicine, computing the probability of X successes can be used to identify the likelihood of a patient developing a certain condition or disease. By understanding the probability of specific outcomes, doctors and medical professionals can develop better treatment plans and improve patient outcomes.
Conclusion of Computing the Probability of X Successes
Computing the probability of X successes is a powerful concept that can be used in a variety of fields and applications. By understanding the likelihood of specific outcomes, we can make informed decisions and improve our chances of success. While this concept can be overwhelming and confusing at times, we hope that this article has provided you with easy-to-understand explanations and insights.
Gallery
Solved 9. Compute The Probability Of X Successes, Using The | Chegg.com
Photo Credit by: bing.com /
Solved Compute The Probability Of X Successes, Using The | Chegg.com
Photo Credit by: bing.com /
Solved Compute The Probability Of X Successes, Using The | Chegg.com
Photo Credit by: bing.com / compute successes probability using binomial formula answer
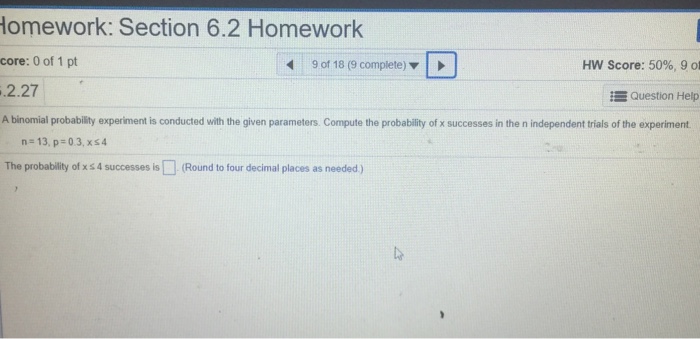
Solved A Binomial Probability Experiment Is Conducted With | Chegg.com
Photo Credit by: bing.com /
Solved 29) Compute The Probability Of X Successes. N=4, X= | Chegg.com
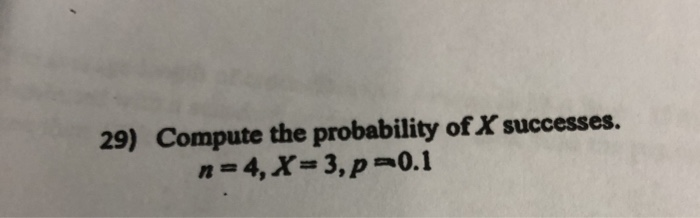
Photo Credit by: bing.com /
