Characteristics Of Normal Probability Curve

Characteristics of normal probability curve

Table of Contents
Pain Points
What is the Empirical Rule and Its Significance?
Skewness and Kurtosis of Normal Probability Curves
Uses of Normal Probability Curves
Question and Answer Section
Q1. What is a normal probability curve?
A. A normal probability curve represents the probability distribution of a random variable that follows a normal distribution. Q2. What is the empirical rule?
A. The empirical rule is a characteristic of normal probability curves that states that approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations of the mean, and 99.7% falls within three standard deviations of the mean. Q3. What are skewness and kurtosis?
A. Skewness refers to the degree of asymmetry of the curve, and Kurtosis is the degree of “peakedness” of the distribution. Q4. What are some common applications of normal probability curves?
A. Common applications of normal curves include demand forecasting, credit scoring, quality control, and hypothesis testing. Conclusion of Characteristics Of Normal Probability Curve
Gallery

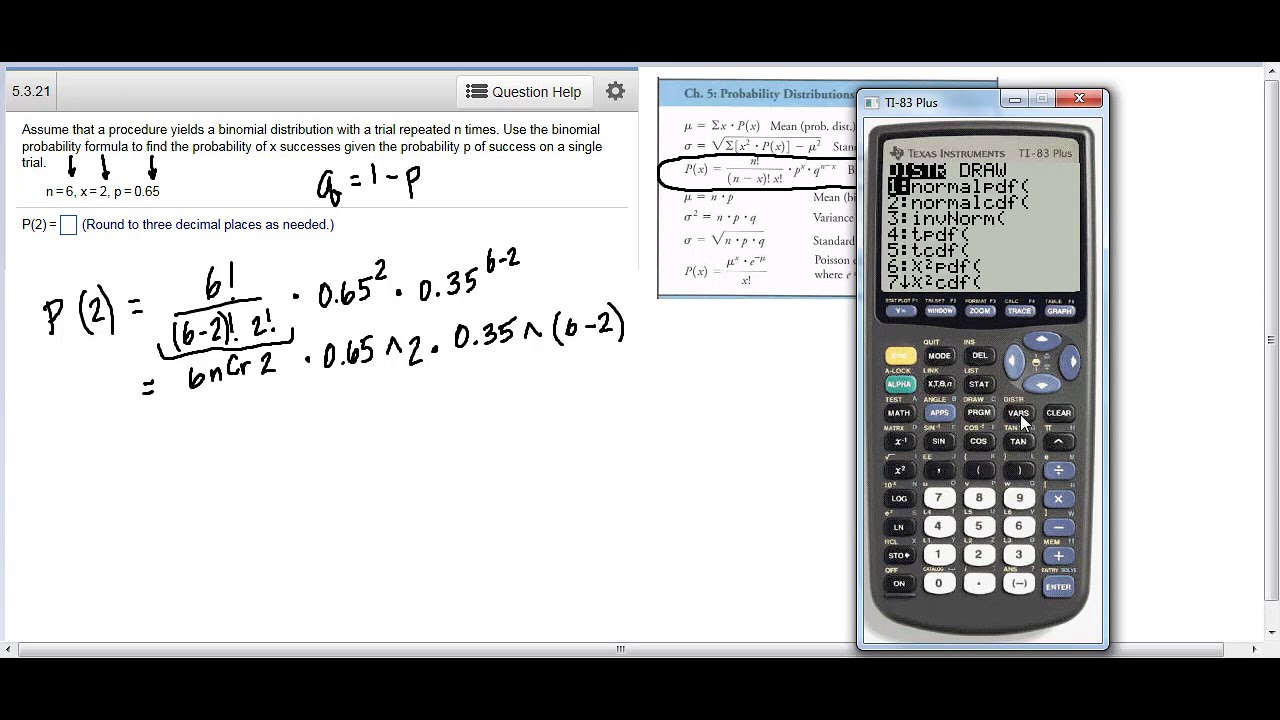
The normal probability curve is a fundamental concept in statistics and data analysis. Understanding the characteristics of this curve is crucial in many fields, including finance, engineering, and social sciences. In this blog post, we dive into the characteristics of normal probability curves, their significance, and ways to interpret them.

Pain Points

Normal probability curves can be challenging to understand and interpret for those who have not studied statistics. Its application in many fields can lead to misinterpretation, resulting in incorrect conclusions. These mistakes can lead to significant financial, legal, or social consequences.

What is the target of Characteristics of Normal Probability Curve?

The target of the characteristics of the Normal Probability Curve is to explain the shape, properties, and importance of this curve in statistics and data analysis. The curve is widely used to model natural phenomena and to compare data in fields such as social sciences, engineering, and finance.

Summary of Main Points

The normal probability curve is a bell-shaped curve that represents the probability distribution of a random variable. It is symmetric around its mean and has certain characteristics that are essential in data analysis and interpretation. These characteristics include the empirical rule, the 68-95-99.7 rule, skewness, and kurtosis. Understanding these properties of normal probability curves is crucial in fields such as finance, engineering, and social sciences.

What is the Empirical Rule and Its Significance?

The empirical rule is one of the critical characteristics of normal probability curves. It states that approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations of the mean, and 99.7% falls within three standard deviations of the mean. This rule is significant in data analysis as it helps to identify outliers that may be due to measurement errors or other factors.

Skewness and Kurtosis of Normal Probability Curves

Skewness and Kurtosis are two other significant characteristics of normal probability curves. Skewness refers to the degree of asymmetry of the curve, and Kurtosis is the degree of “peakedness.” A curve with positive skewness is skewed to the right, while a curve with negative skewness is skewed to the left. Kurtosis can be leptokurtic (more peaked) or platykurtic (less peaked) than a normal distribution.

### Why Skewness and Kurtosis are Important?

Skewness and kurtosis are essential in data analysis as they help in understanding the distribution of the data. Skewed distributions may indicate a potential problem in the data or an opportunity to investigate further. Kurtosis indicates the slope of the distribution’s tails and the degree of outliers.

Uses of Normal Probability Curves

Normal probability curves have numerous applications in various fields such as finance, engineering, social sciences, and data analytics. Common applications of normal curves include demand forecasting, credit scoring, quality control, and hypothesis testing. Normal probability curves are also used in data interpretation and to compare data sets, especially for large samples.

Question and Answer Section

Q1. What is a normal probability curve?
A. A normal probability curve represents the probability distribution of a random variable that follows a normal distribution. Q2. What is the empirical rule?
A. The empirical rule is a characteristic of normal probability curves that states that approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations of the mean, and 99.7% falls within three standard deviations of the mean. Q3. What are skewness and kurtosis?
A. Skewness refers to the degree of asymmetry of the curve, and Kurtosis is the degree of “peakedness” of the distribution. Q4. What are some common applications of normal probability curves?
A. Common applications of normal curves include demand forecasting, credit scoring, quality control, and hypothesis testing. Conclusion of Characteristics Of Normal Probability Curve

The normal probability curve is an essential concept in statistics and data analysis. Its characteristics, including the empirical rule, skewness, and kurtosis, have numerous applications in various fields such as finance, engineering, and social sciences. Understanding the normal probability curve’s properties is crucial in data interpretation and decision-making and can lead to better outcomes.

Gallery