1 experimental theoretical probability multiplication rule
Table of Contents
Table of Contents
Have you ever wondered how to calculate the probability of independent events? You’re not alone! Many people struggle with this concept, but it’s actually quite simple once you understand the basics. In this article, we’ll explore the ins and outs of calculating the probability of independent events and provide some helpful tips along the way.
Pain Points
Understanding probability can be a difficult and daunting task for many people. It can be frustrating trying to wrap your head around concepts like independent events and probability calculations. Additionally, errors in calculations and lack of understanding can lead to incorrect assumptions and choices.
The Target of Calculating Probability of Independent Events
The target of calculating probability of independent events is to determine the likelihood of two or more events occurring independently of one another. In other words, if Event A happens, it does not affect the likelihood of Event B happening. It can be helpful to visualize independent events as two separate experiments with their own set of outcomes.
Main Points
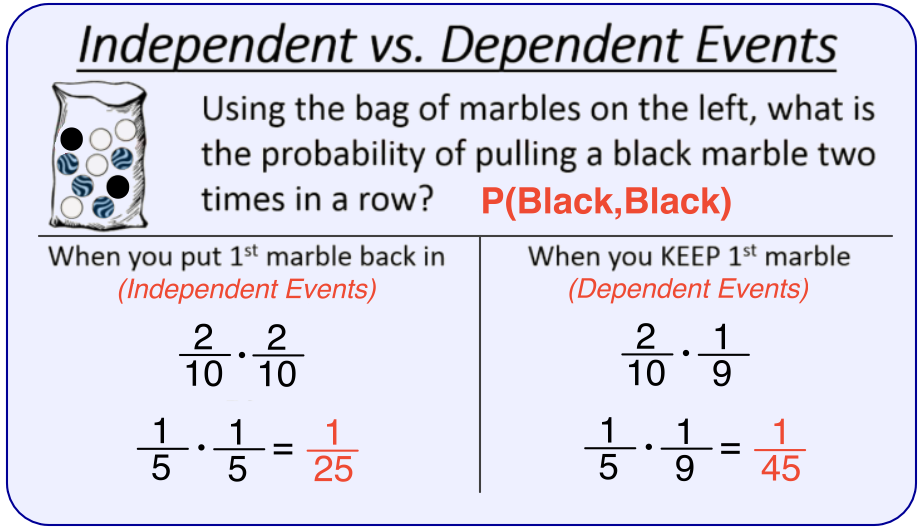
To calculate the probability of independent events, you need to follow a basic formula: P(A and B) = P(A) x P(B). This means that you multiply the probability of Event A by the probability of Event B to arrive at the probability of both events occurring together. Keep in mind that this formula only works for independent events, and not for events that are dependent. Dependent events are those in which the occurrence of one event affects the probability of the other.
Calculating Probability of Independent Events - Personal Experience
I remember struggling with probability in high school. It just didn’t make sense to me! But when we started talking about independent events, it clicked. I realized that sometimes, two events can happen at the same time, even if they are not related. For example, rolling a dice and flipping a coin are two independent events that can happen at the same time. Understanding this helped me immensely in my math classes.
Calculating Probability of Independent Events - Tips
One important thing to keep in mind when calculating the probability of independent events is that the probability of each event must be between 0 and 1. A probability of 0 means that an event will not happen, while a probability of 1 means that an event is certain to happen. Additionally, it’s important to make sure that the events truly are independent. If there is any chance that the occurrence of one event affects the likelihood of the other, then they are not independent!
### The Importance of Precision
Another important aspect of calculating the probability of independent events is precision. It’s important to use the correct equation and to be as accurate as possible when calculating probabilities. Small errors can have big consequences, especially in fields like finance or science where probability is crucial. If you’re unsure about your calculations, always double-check them or seek the advice of a professional.
#### Real-world Applications
Calculating the probability of independent events has numerous real-world applications. For example, it is used in finance to calculate the likelihood of certain investments succeeding or failing. Additionally, probability calculations are used in science to make predictions about the outcome of experiments. Understanding how to calculate the probability of independent events can be incredibly valuable in many different fields.
Question and Answer
Q: What is the formula for calculating the probability of independent events?
A: The formula for calculating the probability of independent events is P(A and B) = P(A) x P(B).
Q: How do I know if events are independent or dependent?
A: Events are independent if the occurrence of one event does not affect the likelihood of the other event occurring. If the occurrence of one event affects the probability of the other event, they are dependent.
Q: Why is precision important when calculating probability?
A: Precision is important when calculating probability because small errors can have big consequences. In fields like finance or science where probability is crucial, accuracy is essential.
Q: What are some real-world applications of calculating the probability of independent events?
A: Probability calculations are used in finance to determine the likelihood of investments succeeding or failing. They are also used in science to make predictions about the outcome of experiments, among other applications.
Conclusion of Calculating Probability Of Independent Events
Calculating the probability of independent events may seem daunting at first, but it’s an essential tool for making predictions and understanding likelihood. By understanding the basics of independent events and using the correct formula, you can make accurate predictions and avoid errors. Whether you’re in the finance industry or studying science, probability calculations are a critical part of your toolkit.
Gallery
Calculating Multiple Event Probabilities - Go Teach Maths: 1000s Of
Photo Credit by: bing.com / multiple event probability probabilities calculating
Probability & Statistics (14 Of 62) The Probability Of A Or B
Photo Credit by: bing.com / probability independent events statistics
Dependent Events (solutions, Examples, Videos)
Photo Credit by: bing.com / probability formulas outcome
Algebra 2 - 10.5 - Probabilities Of Independent And Dependent Events
Photo Credit by: bing.com / dependent independent events algebra probabilities
1) Experimental/Theoretical Probability & Multiplication Rule
Photo Credit by: bing.com / probability multiplication rule events independent dependent calculating theoretical
