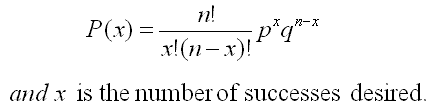Binomial probability distribution tutorial
Table of Contents
Table of Contents
The Binomial Probability Distribution Function is a powerful tool for data analysis. Understanding this mathematical concept can help professionals in many fields make better decisions. Here’s everything you need to know about the Binomial Probability Distribution Function and how you can use it to your advantage.
Potential Pain Points
Without a proper understanding, the Binomial Probability Distribution Function can be overwhelming and intimidating. It involves complex mathematical calculations, and one small mistake can completely change the results. The terminology used in this concept can also be confusing to someone not familiar with it.
What is Binomial Probability Distribution Function?
The Binomial Probability Distribution Function is a mathematical concept that helps in analyzing data consisting of distinct binary outcomes. It provides the probability of the number of successes that can be obtained in a fixed number of repeated independent trials. When the number of trials is very large, and the probability of success is very small, it can be difficult to calculate the probability manually. This is where the Binomial Distribution Function comes in handy.
Summary of Key Points
The Binomial Probability Distribution Function is a mathematical concept that analyzes data consisting of distinct binary outcomes. It helps in determining the probability of the number of successes in a fixed number of repeated independent trials. The function can be intimidating without a proper understanding of the concept and terminology used.
Target and Personal Experience
The target of the Binomial Probability Distribution Function is to analyze data consisting of distinct binary outcomes and calculate the probability of success in a fixed number of repeated independent trials. I remember how I struggled to understand this concept during my statistics course in college. But once I grasped the concept and figured out how to use it effectively, it became a valuable tool for my analysis and decision-making processes.
How to Use Binomial Probability Distribution Function
The Binomial Probability Distribution Function can be used in various fields like finance, economics, healthcare, and more. For example, the Function can be used to calculate the probability of a certain number of patients recovering from a disease when given a specific treatment. In finance, it can be used to calculate the probability of success for a particular investment. Understanding how to use this function can help in making better decisions and predictions based on data analysis.
### Example of Binomial Probability Distribution Function
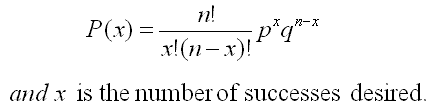
Suppose you are flipping a fair coin ten times, and you want to calculate the probability of getting heads three times. The Binomial Probability Distribution Function can be used to calculate the likelihood of getting heads three times in ten trials. The formula for this calculation is :
P(X=3) = (10!/3!7!) * 0.5^3 * (1-0.5)^7
where:
- P(X=3) represents the probability of getting heads three times in ten trials
- 10! is 10 factorial, which is 10 x 9 x 8 x … x 1
- 3! is 3 factorial, which is 3 x 2 x 1
- (10!/3!7!) is the combination of 10 objects taken 3 at a time
- 0.5 is the probability of getting heads
- (1-0.5) is the probability of getting tails or not getting heads
- ^ represents to the power of
By applying the formula, the probability of getting heads three times in ten trials is 117/512 or 22.85%.
#### Formula for Binomial Probability Distribution Function
The formula for Binomial Distribution Function is :
P(X = k) = (n choose k) * p^k * (1 - p)^(n - k)
where:
- P(X = k) represents the probability of getting ‘k’ successes in ’n’ independent trials
- n choose k is the number of ways of choosing ‘k’ successes among ’n’ trials
- p is the probability of success in each trial
- (1-p) is the probability of failure in each trial
- k can be any integer between 0 and n
Real-Life Example
Suppose a pharmaceutical company wants to test a new drug for efficacy in treating a particular infection. Using the Binomial Probability Distribution Function, the company can calculate the probability of a certain number of cure rates when a specific number of patients are given the drug. This information can help them to decide whether to manufacture the drug or not. Similarly, the marketing department can use this information for their advertising campaign.
Questions and Answers
Q: What is the Binomial Probability Distribution Function used for?
A: The Binomial Probability Distribution Function is used to analyze data consisting of distinct binary outcomes and calculate the probability of success in a fixed number of repeated independent trials
Q: What do the terms ’n’ and ‘p’ represent in the Binomial Probability Distribution Function?
A: ’n’ represents the number of trials, and ‘p’ represents the probability of success in each trial of the Binomial Probability Distribution Function.
Q: How is the Binomial Probability Distribution Function used in finance?
A: In finance, the Binomial Probability Distribution Function can be used to calculate the probability of success for a particular investment.
Q: Can the Binomial Probability Distribution Function be used for non-binary outcomes?
A: No, the function is designed to analyze binary outcomes only.
Conclusion of Binomial Probability Distribution Function
The Binomial Probability Distribution Function is a powerful tool that helps in determining the probability of the number of successes in a fixed number of repeated independent trials. Understanding this function can help professionals in various fields make better decisions and predictions based on data analysis. Although the function can be intimidating at first, with a bit of practice, it can become a valuable tool for any researcher or analyst.
Gallery
Binomial Distribution
Photo Credit by: bing.com / binomial distribution probability function example
PPT - Theoretical Probability Models PowerPoint Presentation - ID:742828
Photo Credit by: bing.com / distribution binomial probability function theoretical models cumulative characteristics ppt powerpoint presentation slideserve
Binomial Probability Distribution - Data Science Kernel
Photo Credit by: bing.com / distribution binomial probability statistics
Binomial Probability Distribution Tutorial
Photo Credit by: bing.com / binomial probability formulas calculate successes onlinemathlearning trials tosses fraction bernoulli roll
PPT - The Binomial Distribution PowerPoint Presentation, Free Download
Photo Credit by: bing.com / binomial distribution formula ppt trials probability general powerpoint presentation number
