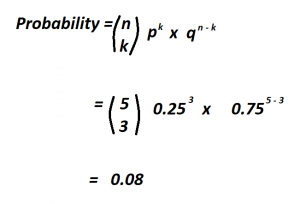Probability by binomial distribution solved numerical problems
Table of Contents
Table of Contents
Are you struggling with Binomial Distribution Probability Problems? Have you been searching for answers to solve these kinds of numerical problems? Look no further, because we have got you covered.
Many students find it challenging to understand and solve problems related to Binomial Distribution Probability, leading to frustration and a lack of confidence in their mathematical abilities. The complex formulas, calculations, and concepts can be overwhelming, making it difficult for anyone to master this topic.
The primary target of Binomial Distribution Probability Problems is to calculate the probability of success or failure in a given number of trials. The problem requires you to use the binomial probability formula, which is P(x) = (nCx)(p^x)(q^(n-x)), where n is the total number of trials, x is the number of successes, p is the probability of success, and q is the probability of failure.
In this article, we will explore Binomial Distribution Probability Problems and related keywords in detail. We will cover various topics, including the binomial probability formula, solving numerical problems, and common mistakes to avoid.
Understanding Binomial Probability Distribution Problems
Binomial Probability Distribution Problems can be tricky, and the best way to master them is by practicing regularly. I recall taking my probability course, and initially, I struggled with solving Binomial Distribution Probability Problems. However, with persistence and practice, I can now solve these problems with ease.
The Binomial Probability Distribution Problems involve calculating the probability of a series of trials when there are only two possible outcomes, namely success or failure. These types of problems usually involve flipping a coin, rolling a dice, or any other binary outcome experiment. In such cases, the probability of success is p, and the probability of failure is q, where q=1-p.
The following image shows a binomial distribution probability problem:
Let’s say we need to find the probability of getting exactly two heads when a coin is flipped five times. In this case, we would use the binomial probability formula to solve the problem, which is:
P(x) = (nCx)(p^x)(q^(n-x))
where n is the total number of trials, x is the number of exact successes we want, p is the probability of success, and q is the probability of failure.
Tips to Solve Binomial Probability Distribution Problems
Solving Binomial Probability Distribution Problems requires a good understanding of the concept, knowledge of the formula, and regular practice. Here are some tips to help you get better at Binomial Probability Distribution Problems:
1. Understand the problem statement: The first step to solving any problem is to understand the problem statement correctly. Make sure you know the total number of trials, the probability of success, and what exactly you are trying to find.
2. Use the Binomial Probability Formula: To solve the problem, use the binomial probability formula P(x) = (nCx)(p^x)(q^(n-x)). Make sure you substitute the values correctly and recheck your calculations.
3. Avoid Common Mistakes: Many students make common mistakes while solving Binomial Probability Distribution Problems, such as using the wrong formula, substituting values incorrectly, or using the wrong units. Always double-check your work to avoid making these common mistakes.
Examples of Binomial Probability Distribution Problems
Here is an example of a Binomial Probability Distribution Problem:
Suppose we want to find the probability of getting at least one six in four rolls of a standard dice. We can use the binomial probability formula to solve the problem:
P(x≥1) = 1- P(x=0) = 1- (4C0)((1/6)^0)((5/6)^(4-0)) = 1- (5/6)^4 = 0.52.
Conclusion of Binomial Distribution Probability Problems
In conclusion, Binomial Distribution Probability Problems can be challenging, but with practice and understanding, anyone can master this concept. Remember to understand the problem statement, use the binomial probability formula correctly, and avoid common mistakes. We hope this article has helped you understand Binomial Distribution Probability Problems and related keywords.
Question and Answer
Q1: What is the Binomial Probability Formula?
A: The Binomial Probability Formula is P(x) = (nCx)(p^x)(q^(n-x)), where n is the total number of trials, x is the number of successes, p is the probability of success, and q is the probability of failure.
Q2: What is the difference between success and failure in Binomial Probability Distribution?
A: In Binomial Probability Distribution, success means the desired outcome, while failure means the opposite of the desired outcome.
Q3: What is the primary target of Binomial Probability Distribution Problems?
A: The primary target of Binomial Probability Distribution Problems is to calculate the probability of success or failure in a given number of trials.
Q4: What are the common mistakes made while solving Binomial Probability Distribution Problems?
A: Some common mistakes made while solving Binomial Probability Distribution Problems are using the wrong formula, substituting values incorrectly, and using the wrong units.
Gallery
5 Iv. Binomial Probability Distribution Problem. - YouTube
Photo Credit by: bing.com / binomial distribution probability problem
Chapter 5.2 “Binomial Probability Distribution” - YouTube
Photo Credit by: bing.com / binomial distribution probability
Probability By Binomial Distribution: Solved Numerical Problems
Photo Credit by: bing.com / probability binomial statistics interview solved mathematics
Binomial Distribution (examples, Solutions, Formulas, Videos)
Photo Credit by: bing.com / binomial distribution formula formulas examples equation solutions distributions stats videos questions introduction
Binomial Distribution (Fully Explained W/ 11 Examples!)
Photo Credit by: bing.com / binomial probability distribution example examples
