Bayes Theorem Of Probability

Bayes theorem solutions formulas examples videos

Table of Contents

Have you ever heard of Bayes Theorem of Probability? It may sound complex, but it’s actually a powerful tool used in various fields to make predictions and solve problems. Understanding Bayes Theorem can give you a valuable advantage in decision making, data analysis, and more.

Identifying Pain Points Related to Bayes Theorem of Probability

Bayes Theorem of Probability can be confusing and overwhelming, especially for those who are new to it. It can be challenging to understand the concept and how it applies to real-world situations. Moreover, some people may find it difficult to compute the probability values and use them to make informed decisions.

What is Bayes Theorem of Probability?

Bayes Theorem of Probability is a mathematical formula that calculates conditional probability. It is named after Reverend Thomas Bayes, an 18th-century statistician, and philosopher. The formula describes the probability of an event based on prior knowledge or information that is updated with new data or evidence.

Key Points about Bayes Theorem of Probability and Related Keywords

Bayes Theorem is based on conditional probability, which means the probability of an event occurring given that another event has already happened. It requires prior knowledge or information, which is known as the prior probability, to compute the likelihood of an event occurring. Bayes Theorem can be used in various fields, including medicine, finance, and engineering, to make predictions and decisions based on updated information.

My Personal Experience with Bayes Theorem of Probability

When I first learned about Bayes Theorem, I was intimidated by the complex formula and its application. However, with the help of examples and practice problems, I was able to understand how it works and how it can be useful in solving real-world problems. Bayes Theorem has helped me make informed decisions, predict outcomes, and analyze data with more accuracy.

Applying Bayes Theorem of Probability in Real Life

Bayes Theorem of Probability has endless applications in various fields. For example, in medicine, Bayes Theorem can be used to diagnose diseases and predict the effectiveness of treatments. In finance, it can help investors make decisions based on updated market information. In engineering, it can be used to predict the failure of a product and improve its design.

Understanding the Formula of Bayes Theorem of Probability and Related Keywords

The formula of Bayes Theorem of Probability is as follows: P(A|B) = (P(B|A) x P(A)) / P(B) where:

• P(A|B) is the probability of A given that B has occurred
• P(B|A) is the probability of B given that A has occurred
• P(A) is the prior probability of A
• P(B) is the prior probability of B

By using this formula, we can calculate the probability of an event occurring based on updated information or evidence.

Examples of Bayes Theorem of Probability in Action

Let’s say you are a doctor trying to diagnose a rare disease. According to statistics, the disease affects 0.1% of the population. You conduct a test that is 95% accurate, meaning it correctly identifies 95% of the cases and incorrectly identifies 5% of the healthy patients as positive. If the test comes back positive, what is the probability that the patient has the disease?

Using Bayes Theorem of Probability, we can calculate:

• P(Disease) = 0.001 (the prior probability)
• P(Positive|Disease) = 0.95 (the probability that the test is positive given that the patient has the disease)
• P(Negative|No Disease) = 0.95 (the probability that the test is negative given that the patient does not have the disease)
• P(No Disease) = 0.999 (the probability that the patient does not have the disease)

Using the Bayes Theorem formula, we can calculate:

• P(Disease|Positive) = (0.95 x 0.001) / ((0.95 x 0.001) + (0.05 x 0.999)) = 0.016 = 1.6%

Therefore, the probability that the patient has the disease is only 1.6%, despite the positive test result.

Question and Answer about Bayes Theorem of Probability

Q. What is the difference between Bayesian Inference and Bayes Theorem of Probability?

A. Bayes Theorem is a mathematical formula that calculates conditional probability, whereas Bayesian Inference is a statistical method that uses Bayes Theorem to update probability estimates based on data or evidence.

Q. What are the limitations of Bayes Theorem of Probability?

A. Bayes Theorem assumes that the prior probabilities are known and accurate, which can be challenging to estimate in some cases. It also assumes that the events are independent, which may not always be true in real-world situations.

Q. How is Bayes Theorem used in Data Science?

A. Bayes Theorem is used in Data Science to update probability distributions and make predictions based on new data or evidence. It is used in Bayesian Statistics, Machine Learning, and Artificial Intelligence to model complex systems and make informed decisions.

Q. Is Bayes Theorem only used in Mathematics and Statistics?

A. No, Bayes Theorem has various applications in different fields, including but not limited to Medicine, Finance, Epidemiology, Engineering, and Computer Science.

Conclusion of Bayes Theorem of Probability

Bayes Theorem of Probability is a powerful tool that can help make informed decisions, predictions, and solve problems in various fields. Understanding the formula and its applications can give you a competitive advantage in your career or personal life. Although it may seem daunting at first, with practice and examples, you can master this useful mathematical concept.

Gallery

Bayes Theorem - Statement, Proof, Formula, Derivation & Examples

_{^{Photo Credit by: bing.com / bayes theorem proof probability examples formula conditional statement derivation maths}}

PPT - PROBABILITY - Bayes’ Theorem PowerPoint Presentation, Free

_{^{Photo Credit by: bing.com / bayes theorem probability ppt conditional prior posterior application probabilities computation information powerpoint presentation}}

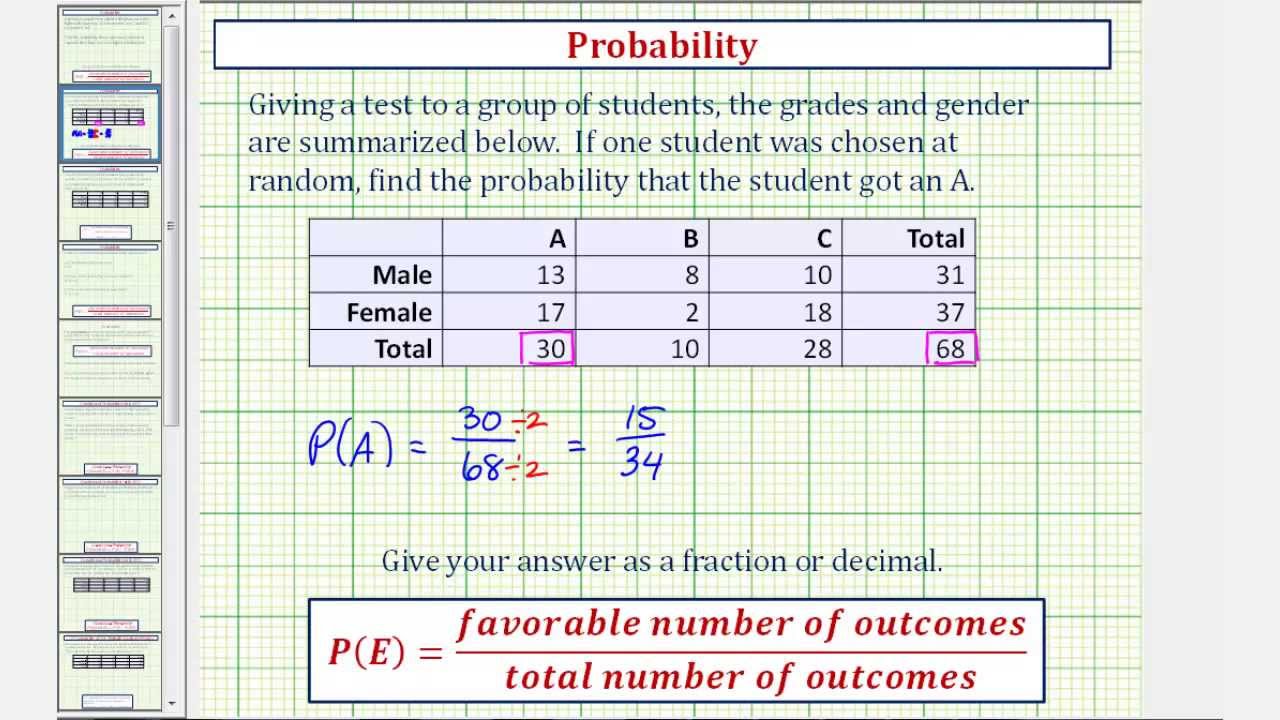
Bayes Theorem (solutions, Formulas, Examples, Videos)

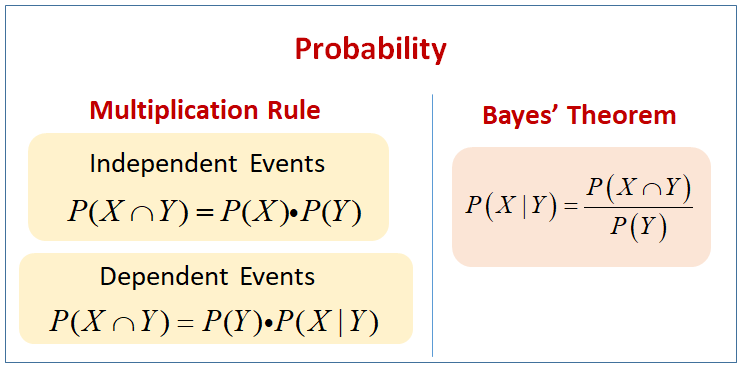
_{^{Photo Credit by: bing.com / bayes theorem probability multiplication events rules solutions law independent addition examples intersection formulas dependent using}}

PPT - PROBABILITY - Bayes’ Theorem PowerPoint Presentation, Free

_{^{Photo Credit by: bing.com / bayes theorem probability conditional ppt formula definition event probabilities powerpoint presentation}}

Image – Bayes’ Theorem

_{^{Photo Credit by: bing.com / bayes rule bayesian naive theorem statistics learning spam probabilities probabilistic sophistication classifiers ironic classifier}}