Bayes theorem probability conditional ppt formula definition event probabilities powerpoint presentation
Table of Contents
Table of Contents
Have you ever been uncertain about the likelihood of an event occurring? Maybe you’re trying to predict the weather for an upcoming picnic or estimate the probability of a coin landing on heads. These situations involve conditional probabilities, and Bayes Theorem Conditional Probability is a useful tool to help make these predictions and estimations. In this blog post, we’ll explore what Bayes Theorem Conditional Probability is and how it can be used to make more accurate predictions and estimations.
The Pain Points of Uncertainty
Uncertainty can be frustrating and can lead to poor decision making. Without reliable information about the likelihood of events, we may make choices that ultimately lead to negative outcomes. For example, if we don’t know the probability of rain for a picnic, we may not bring adequate shelter or cancel the event altogether. These uncertainties can be especially challenging in fields like finance and healthcare, where decisions can have high stakes consequences.
The Target of Bayes Theorem Conditional Probability
Bayes Theorem Conditional Probability is a statistical formula that helps us to update probabilities as we gain new information. Simply put, it helps us to make predictions based on prior knowledge and new evidence. The formula involves calculating the probability of an event given the occurrence of another related event. The target is to use Bayes Theorem to revise the probability of an event occurring, taking into account any new information.
Summary
In summary, Bayes Theorem Conditional Probability is a statistical tool that enables us to make more accurate predictions in the face of uncertainty. By considering prior knowledge and incorporating new information, the formula allows us to update our estimates of the likelihood of an event occurring. In the next sections, we’ll dive deeper into how the formula works and explore some practical examples of its use.
Understanding Bayes Theorem Conditional Probability
Bayes Theorem Conditional Probability can be explained through a simple example. Imagine that a doctor is trying to diagnose a patient with a rare disease. The doctor knows that the disease affects 1 in 1000 people, or 0.1%. The doctor also knows that the diagnostic test for the disease is 95% accurate, with a 5% false positive rate. The patient takes the test, and it comes back positive. What is the probability that the patient actually has the disease?
 Using Bayes Theorem, the probability that the patient has the disease given a positive test result can be calculated. The formula for Bayes Theorem is:
Using Bayes Theorem, the probability that the patient has the disease given a positive test result can be calculated. The formula for Bayes Theorem is:
P(A | B) = P(B | A) x P(A) / P(B)
Where:
- P(A | B) is the probability of A given B
- P(B | A) is the probability of B given A
- P(A) is the prior probability of A
- P(B) is the prior probability of B
In the example, A is the presence of the rare disease, and B is the positive test result. Using the information we have, we can calculate the probabilities:
- P(A) = 0.1% or 0.001
- P(B | A) = 95% or 0.95 (the probability of a positive test given the patient has the disease)
- P(¬A) = 99.9% or 0.999 (the probability of not having the disease)
- P(B | ¬A) = 5% or 0.05 (the probability of a false positive)
Now we can plug these values into the Bayes Theorem formula:
P(A | B) = P(B | A) x P(A) / P(B | A) x P(A) + P(B | ¬A) x P(¬A)
P(A | B) = 0.95 x 0.001 / 0.95 x 0.001 + 0.05 x 0.999
P(A | B) = 0.01825 or 1.83%
This calculation shows that even with a positive test result, there is still only a 1.83% chance that the patient actually has the rare disease. This example highlights the key concept of Bayes Theorem: the importance of prior knowledge when updating probabilities with new evidence.
Applying Bayes Theorem Conditional Probability to Finance
Bayes Theorem Conditional Probability can equally be used in other fields, such as finance. For example, a stock trader may use Bayes Theorem to adjust their probability estimates of a company’s stock price based on new information, such as a news announcement or quarterly earnings report. By using Bayes Theorem, they can incorporate prior knowledge of the company and industry to update their estimates and make better investment decisions.
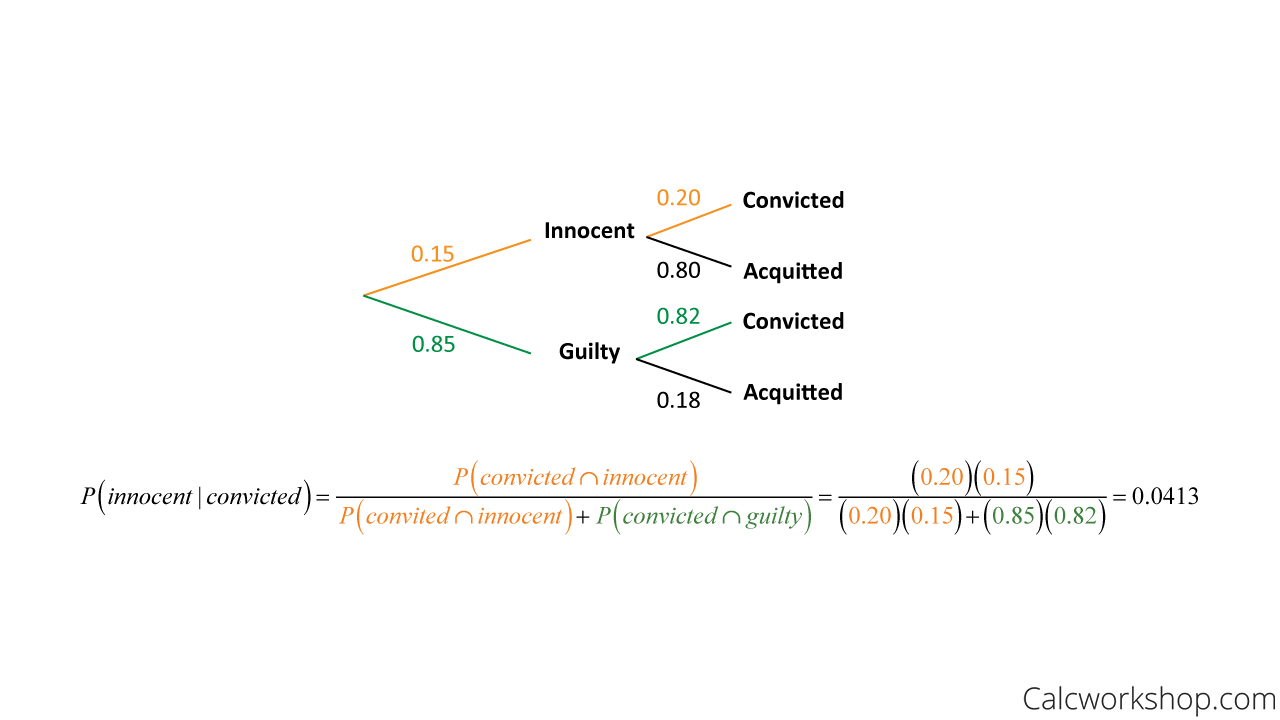 ### The Importance of Prior Knowledge
### The Importance of Prior Knowledge
One of the key strengths of Bayes Theorem Conditional Probability is its ability to incorporate prior knowledge. This prior knowledge can be a combination of historical data, expert opinions, and domain knowledge. This is especially important in situations where there is limited data, and the uncertainties are high. By leveraging prior knowledge, we can make better predictions and reduce the impact of uncertainty on our decision making.
In Practice: Bayesian Networks
A Bayesian network is a graphical model that represents probabilistic relationships among a set of variables and their conditional dependences. These networks are used in many fields, including finance, healthcare, and engineering, to model complex systems and make probabilistic predictions. Bayesian networks are built using Bayes Theorem Conditional Probability as the foundation, making them a powerful tool for decision makers.
Question and Answer
1. What is Bayes Theorem Conditional Probability?
Bayes Theorem Conditional Probability is a statistical formula that helps to update probabilities as we gain new information. It involves calculating the probability of an event given the occurrence of another related event.
2. Why is Bayes Theorem Conditional Probability important?
Bayes Theorem Conditional Probability is important as it enables us to make better predictions in the face of uncertainty. By incorporating prior knowledge and new information, we can update our estimates and reduce the impact of uncertainty on our decision making.
3. How is Bayes Theorem Conditional Probability used in finance?
Bayes Theorem Conditional Probability can be used in finance to adjust probability estimates of an investment’s return, based on new information that becomes available. By using prior knowledge of the investment’s history and market trends, investors can make better decisions about their portfolios.
4. What is a Bayesian network?
A Bayesian network is a graphical model that represents probabilistic relationships among a set of variables and their conditional dependences. It is a powerful tool used in many fields to model complex systems and make probabilistic predictions.
Conclusion of Bayes Theorem Conditional Probability
Bayes Theorem Conditional Probability is a powerful tool for decision-making in uncertain environments. By incorporating prior knowledge and new information, we can improve our predictions and reduce uncertainty’s negative impact on our decision making. From finance to healthcare, Bayes Theorem Conditional Probability is applied in many fields, making it a valuable tool for any decision maker.
Gallery
PPT - PROBABILITY - Bayes’ Theorem PowerPoint Presentation, Free

Photo Credit by: bing.com / bayes theorem probability conditional ppt formula definition event probabilities powerpoint presentation
Bayes Theorem (Easily Explained W/ 7 Examples!)

Photo Credit by: bing.com / bayes theorem probability conditional easily
Bayes Theorem Conditional Probability Proof Along With Solved Examples

Photo Credit by: bing.com / probability conditional bayes theorem proof examples solved conditions maths
Bayes Theorem - Statement, Proof, Formula, Derivation & Examples

Photo Credit by: bing.com / bayes theorem proof probability examples formula conditional statement derivation maths
Bayes’ Rule With A Simple And Practical Example | By Tirthajyoti Sarkar
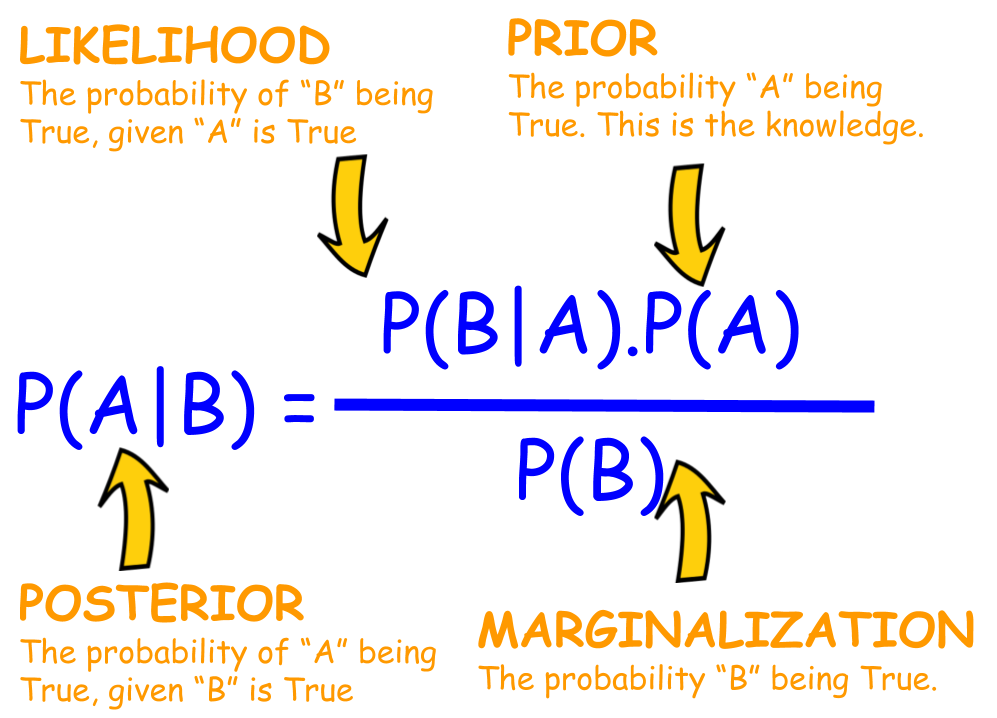
Photo Credit by: bing.com / bayes bayesian example rule simple statistics theorem probability prior probabilities reasoning practical logic using thinking data model disease